Discriminant analysis

Let's suppose we consider a multi-class classification problem where the conditional probability for a sample x_i ∈ ℜ^m to belong to the y_j class can be modeled as a multivariate Gaussian distribution (X is assumed to be made up of independent and identically distributed (i.i.d) variables with extremely low collinearities):

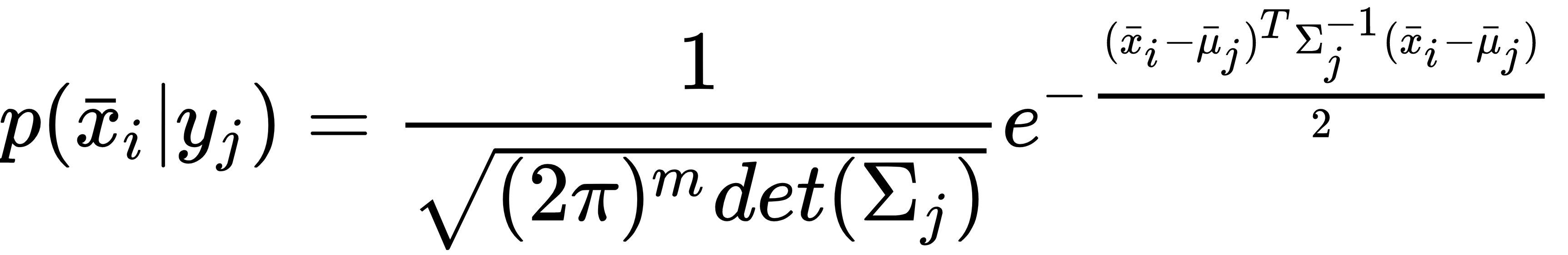
In this case, the class j is fully determined by the mean vector μ_j and the covariance matrix Σ_j. If we apply the Bayes' theorem, we can obtain the posterior probability p(y_j|x_i):

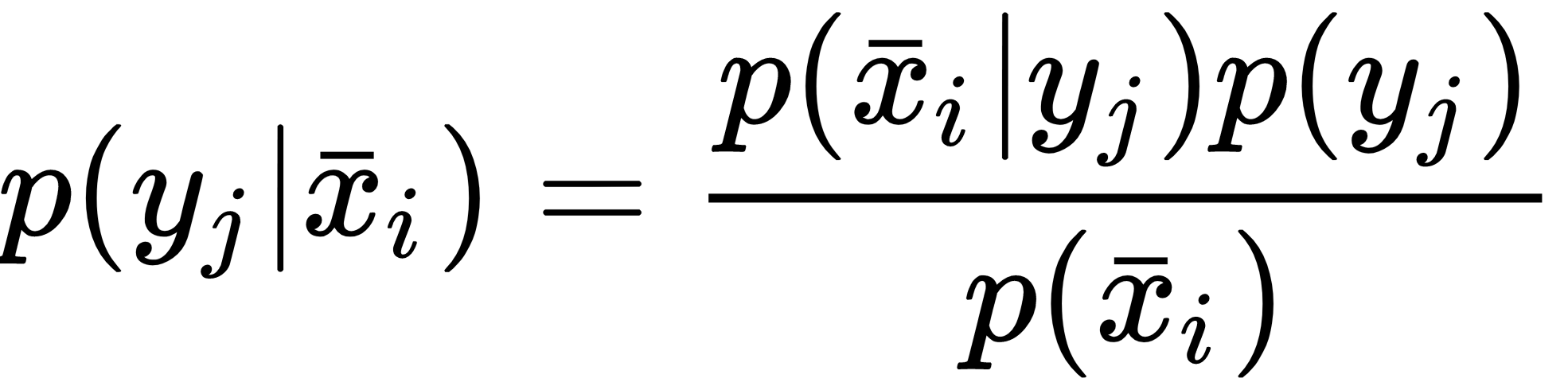
Considering the discussion of Gaussian Naive Bayes, it's not difficult to understand how it's possible to estimate μ_j and Σ_j using the training set, in fact, they correspond to the sample mean and covariance and can be easily computed in closed form.

Now, for simplicity, let's consider a binary problem...