Examining temperature and velocity distribution of particles
A system at thermal equilibrium at a constant temperature T is characterized by its Maxwell-Boltzmann velocity distribution. According to this distribution, the probability distribution 
of velocities in a single direction i (which can be x, y, z) of a system of particles of mass m each is given by the Gaussian function, illustrated here in Figure 1.2:
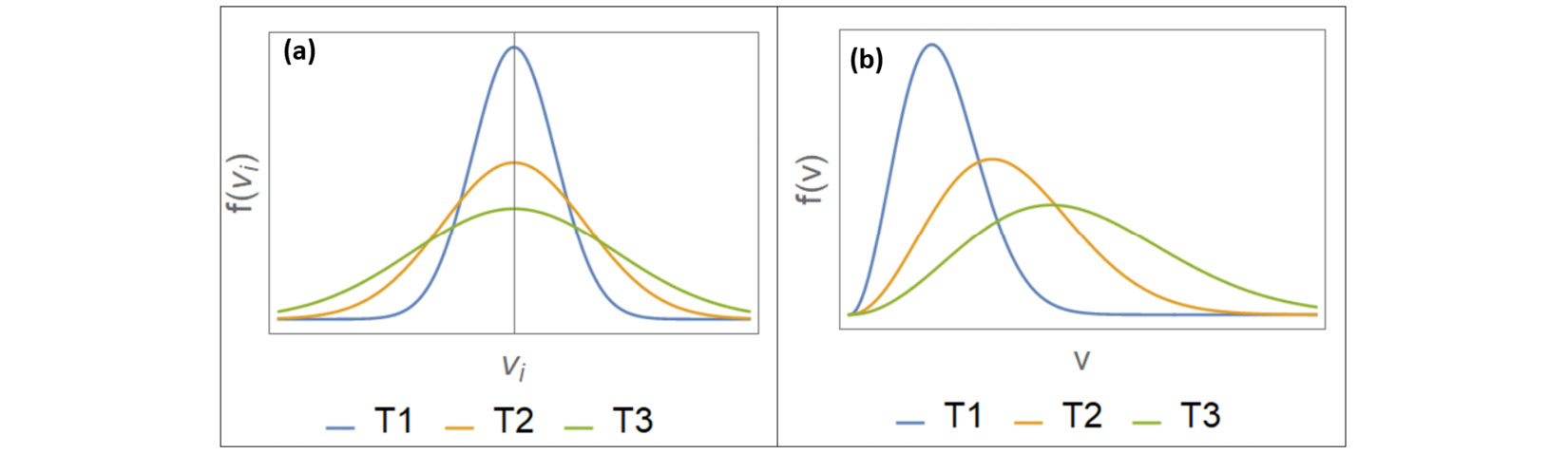
Figure 1.2 – The Maxwell-Boltzmann velocity distributions (left) and speed distributions (right)
The preceding graph is plotted for the same system at three different temperatures 
.
The corresponding functional form that depends on the mass and temperature is shown here:
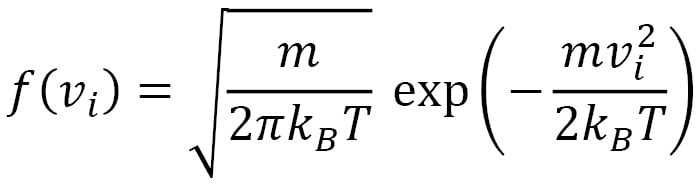
Here, 
is the Boltzmann constant. This distribution has a mean of 
and a standard deviation of 
. The shape of the Gaussian curve is determined by the ratio of 
. The velocity distribution of the velocity vector 
is given by the following formula:
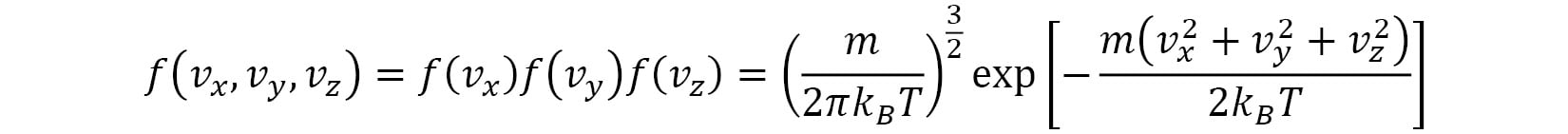
In spherical coordinates, this distribution can be written in terms of the speed 
, as follows:
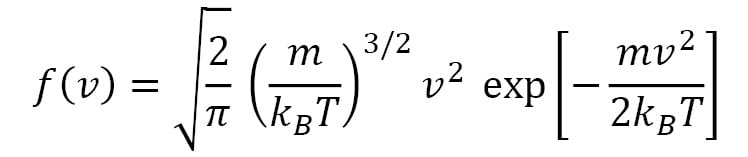
This is the Maxwell-Boltzmann speed distribution, also known as a Rayleigh distribution. The shape of the speed distribution changes with temperature, as shown in Figure 1.2, and the peak speed increases with temperature. The velocity distributions are wider at higher temperatures, and the speed distributions show larger peak speeds at higher temperatures. An algorithm that controls temperature in a molecular simulation must account for the preceding features regarding particle velocities.
So far, concepts that dictate the operation of an MD simulation have been discussed. These concepts are implemented in a computational environment through codes that will be discussed in later chapters. In the next section, we will discuss related computational concepts that are commonly encountered in MD simulations and that are prevalently used to enhance simulation performance.
