Cauchy-Schwarz and triangle inequalities
The Cauchy-Schwarz inequality is one of the most important inequalities in mathematics. Succinctly stated, it says that the absolute value of the inner product of two vectors is less than or equal to the norm of those two vectors multiplied together. In fact, they are only equal if the two vectors are linearly dependent:
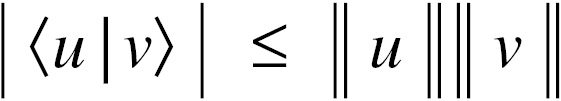
There are several proofs of this inequality, which I encourage you to seek out if you are interested. But, in the totality of things, knowing this inequality is all that is really required for quantum computing.
The other major inequality is the triangle inequality. It comes from our old friend Euclid in his book The Elements. Succinctly stated, it says that the length of two sides of a triangle must always be more than the length of one side. They will only be equal in the corner case when the triangle has zero area. It is very intuitive once you see some example triangles. Here are some triangles...






















































