Now we'll move on to discussing Bayesian methods for analyzing the means of quantitative data. This section is similar to the previous one on Bayesian methods for analyzing proportions, but it focuses on the means of quantitative data. Here, we look at constructing credible intervals and performing hypothesis testing.
Suppose that we assume that our data was drawn from a normal distribution with an unknown mean, μ, and an unknown variance, σ2. The conjugate prior, in this case, will be the normal inverse gamma (NIG) distribution. This is a two-dimensional distribution, and gives a posterior distribution for both the unknown mean and the unknown variance.
In this section, we only care about what the unknown mean is. We can get a marginal distribution for the mean from the posterior distribution, which depends only on the mean. The variance no longer appears in the marginal distribution. We can use this distribution for our analysis.
So, we say that the mean and the standard deviation, both of these things being unknown, were drawn from a NIG distribution with the parameters of μ0, μ, α, and β. This can be represented using the following formula:
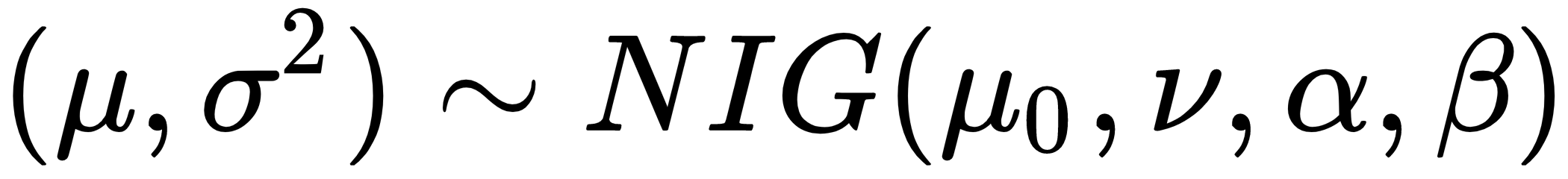
The posterior distribution after you have collected data can be represented as follows:
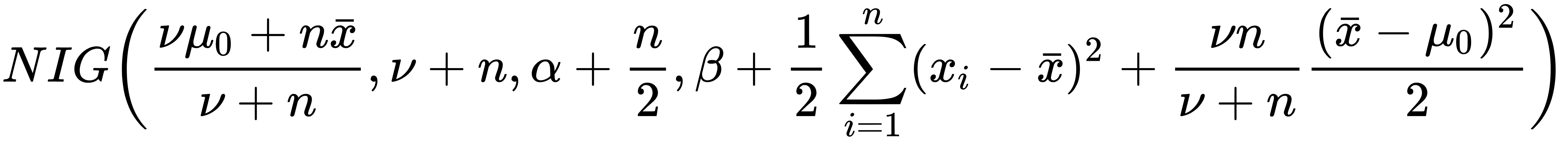
In this case, I'm interested in the marginal distribution of the mean, μ, under the posterior distribution. The prior marginal distribution of μ is t(2α), which means that it follows a t-distribution with two alpha degrees of freedom; this is the posterior marginal distribution of the following formula:
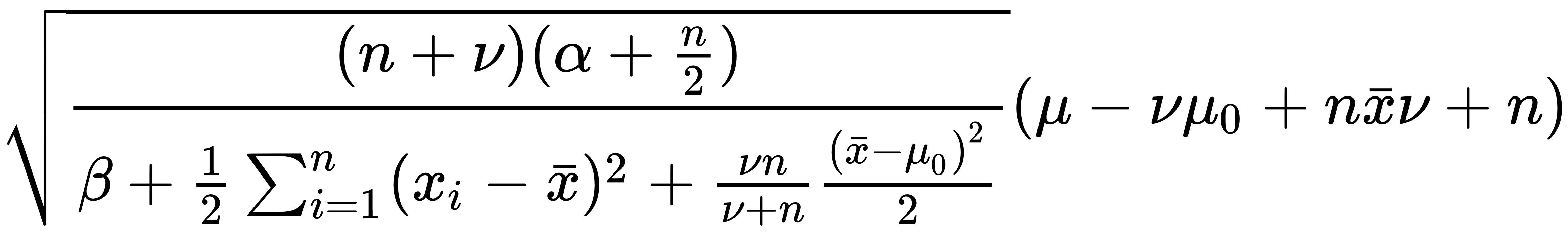
Here, it is t(2α + n).
This is all very complicated, so I've written five helper functions, which are as follows:
- Compute the probability density function (PDF) of (μ,σ2), which is useful for plotting.
- Compute the parameters of the posterior distribution of (μ,σ2).
- Compute the PDF and CDF of the marginal distribution of μ (for either the prior or posterior distribution).
- Compute the inverse CDF of the marginal distribution of μ (for either the prior or posterior distribution).
- Simulate a draw from the marginal distribution of μ (for either the prior or posterior distribution).
We will apply these functions using the following steps:
- So, first, we're going to need these libraries:
- Then, the dnig() function computes the density of the normal inverse gamma distribution—this is helpful for plotting, as follows:

- The get_posterior_nig() function will get the parameters of the posterior distribution, where x is our data; and these four parameters specify the parameters of the prior distribution, but will be returned as a tuple that contains the parameters of the posterior distribution:

- The dnig_mu_marg() function is the density function of the marginal distribution for μ. It will be given a floating-point number that you want to evaluate the PDF on. This will be useful if you want to plot the marginal distribution of μ:

- The pnig_mu_marg() function computes the CDF of the marginal distribution; that is, the probability of getting a value less than or equal to your value of x, which you pass to the function. This'll be useful if you want to do things such as hypothesis testing or computing the probability that a hypothesis is true under the posterior distribution:

- The qunig_mu_marg() function will be the inverse CDF, however, you give it a probability, and it will give you the quantile associated with that probability. This is a function that's going to be useful if you want to construct, say, credible intervals:

- Finally, the rnig_mu_marg() function draws random numbers from the marginal distribution of μ from a normal inverse gamma distribution, so this'll be useful if you want to sample from the posterior distribution of μ:

- Now, we will perform a short demonstration of what the dnig() function does, so you can get an idea of what the normal inverse gamma distribution looks like, using the following code:
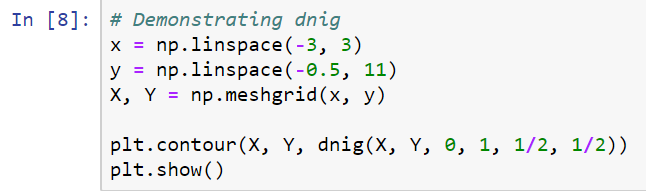
This results in the following output:
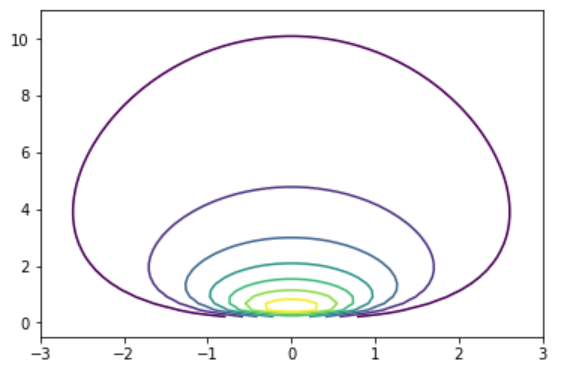
This plot gives you a sense of what the normal inverse gamma looks like. Therefore, most of the density is concentrated in this region, but it starts to spread out.















































































