Bayesian statistics isn't just another method. It is an entirely different paradigm for practicing statistics. It uses probability models for making inferences, given the data that has been collected. This can be expressed in a fundamental expression as P(H|D).
Here, H is our hypothesis, that is, the thing we're trying to prove, and D is our data or observations.
As a reminder of our previous discussion, the diachronic form of Bayes' theorem is as follows:
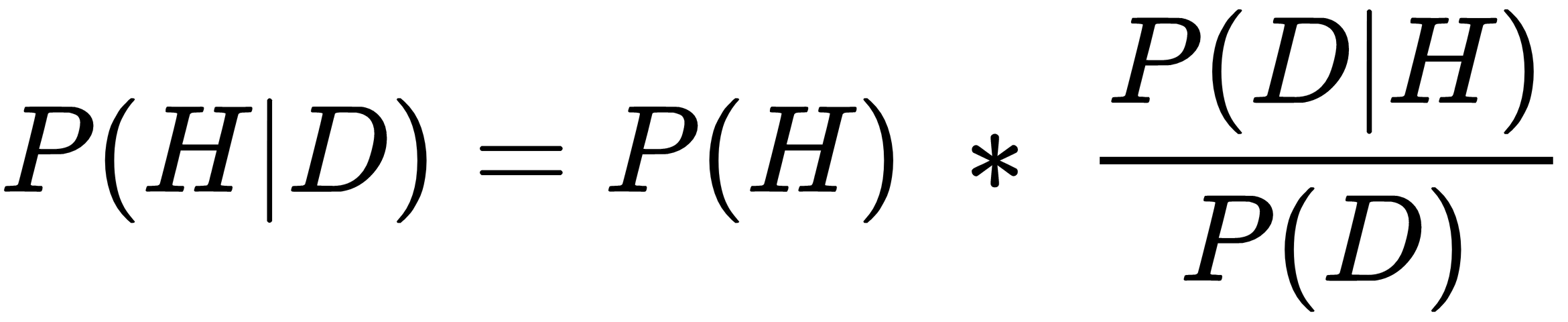
Here, P(H) is an unconditional prior probability that represents what we know before we conduct our trial. P(D|H) is our likelihood function, or probability of obtaining the data we observe, given that our hypothesis is true.
P(D) is the probability of the data, also known as the normalizing constant. This can be obtained by integrating the numerator...


























































