Up until now, we have seen how the applications of AR and MA are processed separately. However, in some cases, combining the two allows us to handle more complex time series data. The ARMA model is a combination of the AR(p) and MA(q) processes and can be written as follows:
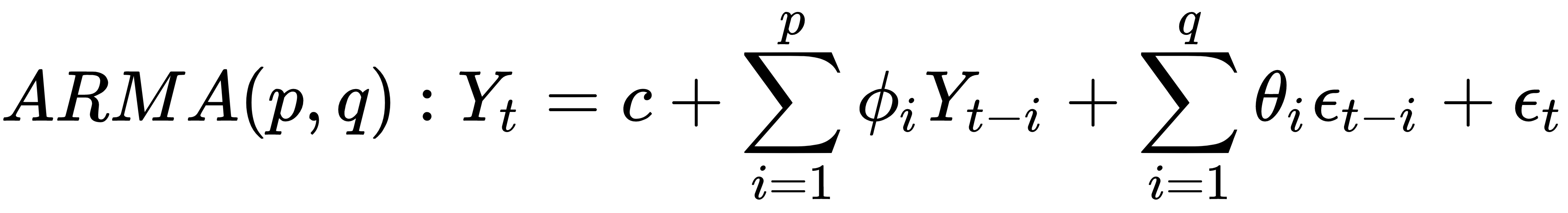
The following terms are used in the preceding equation:
- ARMA(p,q) defines an ARMA process with a p-order AR process and q-order moving average process
- Yt represents the series itself
- c represents a constant (or drift)
- p defines the number of lags to regress against Yt
 is the coefficient of the i lag of the series
is the coefficient of the i lag of the series- Yt-1 is the i lag of the series
- q defines the number of past error terms to be used in the equation
 is the corresponding coefficient of
is the corresponding coefficient of 
 are white noise error terms
are white noise error terms represents the error term, which is white noise
represents the error term, which is white noise
For instance, an ARMA(3,2) model is defined by the following equation...












































































