The objective function for this problem is similar to the objective function defined earlier for the single-pole balancing problem. It is given by the following equations:
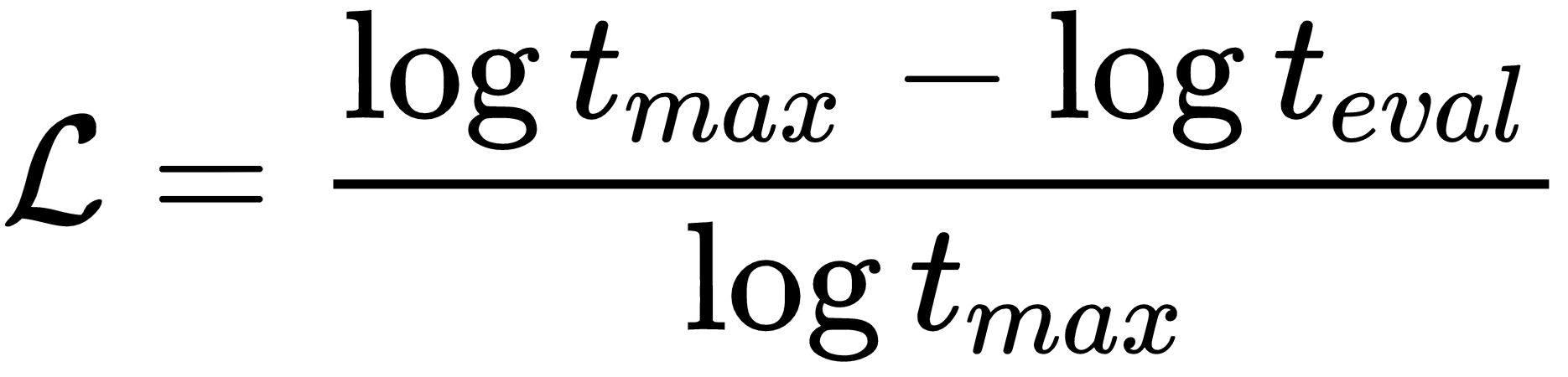
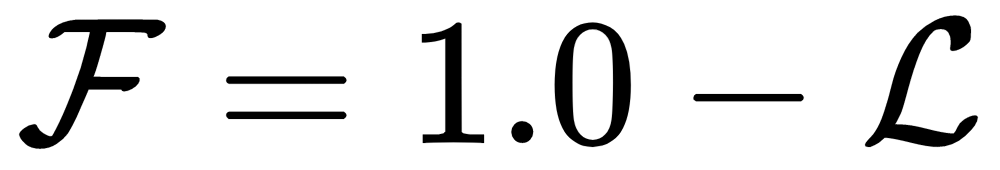
In these equations,  is the expected number of time steps specified in the configuration of the experiment (100,000), and
is the expected number of time steps specified in the configuration of the experiment (100,000), and  is the actual number of time steps during which the controller was able to maintain a stable state of the pole balancer within the specified limits.
is the actual number of time steps during which the controller was able to maintain a stable state of the pole balancer within the specified limits.
We use logarithmic scales because most of the trials fail in the first several 100 steps, but we are testing against 100,000 steps. With a logarithmic scale, we have a better distribution of fitness scores, even compared with a small number of steps in failed trials.
The first of the preceding equations defines the loss, which is in the [0,1] range, and the second is a fitness score...


































































