Graphs can be represented as large matrices pretty easily. The first technique we are going to study that can reduce the size of this matrix is called matrix factorization.
The adjacency matrix and graph Laplacian
Similar to text analysis, graphs can be represented by a very large matrix encoding the relationships between nodes. We have already used such a matrix in the preceding chapters – the adjacency matrix, named M in the following diagram:
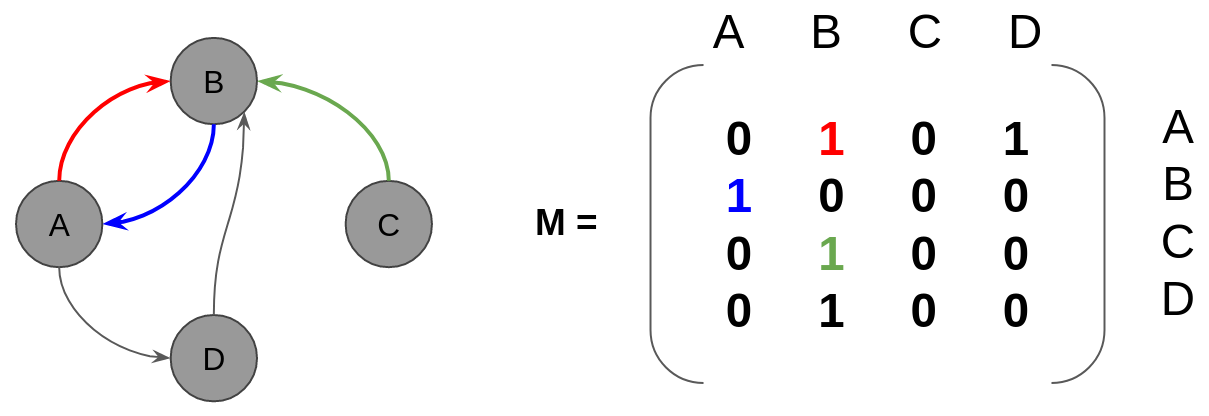
Other algorithms rely on the graph Laplacian matrix L = D - M where D is the diagonal matrix containing the degree of each node. But the principles remain unchanged.
Eigenvectors embedding
One simple way of reducing the size of the matrix is to decompose it into eigenvectors, and use only a reduced number of these vectors as embedding.
An example of such graph representation can be seen when using graph positioning. Indeed, drawing a graph on a two-dimensional plane is a type of embedding. One of the positioning...























































