Chapter 6: Graph Algorithms I
Activity 13: Finding out Whether a Graph is Bipartite Using DFS
In this activity, we will check whether a graph is bipartite using depth-first search traversal. Follow these steps to complete the activity:
- Add the required header files and declare the graph to be used:
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <stack>
template<typename T> class Graph;
- Write the following struct to define an edge in our graph:
template<typename T>
struct Edge
{
size_t src;
size_t dest;
T weight;
// To compare edges, only compare their weights,
// and not the source/destination vertices
inline bool operator< (const Edge<T>& e) const
{
return this->weight < e.weight;
}
inline bool operator> (const Edge<T>& e) const
{
return this->weight > e.weight;
}
};
- Use the following function to overload the << operator for the graph so that it can be written to standard output:
template <typename T>
std::ostream& operator<<(std::ostream& os, const Graph<T>& G)
{
for (auto i = 1; i < G.vertices(); i++)
{
os << i << ":\t";
auto edges = G.outgoing_edges(i);
for (auto& e : edges)
os << "{" << e.dest << ": " << e.weight << "}, ";
os << std::endl;
}
return os;
}
- Implement the edge list graph as follows:
template<typename T>
class Graph
{
public:
// Initialize the graph with N vertices
Graph(size_t N) : V(N)
{}
// Return number of vertices in the graph
auto vertices() const
{
return V;
}
// Return all edges in the graph
auto& edges() const
{
return edge_list;
}
void add_edge(Edge<T>&& e)
{
// Check if the source and destination vertices are within range
if (e.src >= 1 && e.src <= V &&
e.dest >= 1 && e.dest <= V)
edge_list.emplace_back(e);
else
std::cerr << "Vertex out of bounds" << std::endl;
}
// Returns all outgoing edges from vertex v
auto outgoing_edges(size_t v) const
{
std::vector<Edge<T>> edges_from_v;
for (auto& e : edge_list)
{
if (e.src == v)
edges_from_v.emplace_back(e);
}
return edges_from_v;
}
// Overloads the << operator so a graph be written directly to a stream
// Can be used as std::cout << obj << std::endl;
template <typename T>
friend std::ostream& operator<< <>(std::ostream& os, const Graph<T>& G);
private:
size_t V; // Stores number of vertices in graph
std::vector<Edge<T>> edge_list;
};
- Create the graph shown in figure 6.17, as shown here:
template <typename T>
auto create_bipartite_reference_graph()
{
Graph<T> G(10);
std::map<unsigned, std::vector<std::pair<size_t, T>>> edges;
edges[1] = { {2, 0} };
edges[2] = { {1, 0}, {3, 0} , {8, 0} };
edges[3] = { {2, 0}, {4, 0} };
edges[4] = { {3, 0}, {6, 0} };
edges[5] = { {7, 0}, {9, 0} };
edges[6] = { {1, 0}, {4, 0} };
edges[7] = { {5, 0} };
edges[8] = { {2,0}, {9, 0} };
edges[9] = { {5, 0} };
for (auto& i : edges)
for (auto& j : i.second)
G.add_edge(Edge<T>{ i.first, j.first, j.second });
return G;
}
- Now, we need a function so that we can implement our algorithm and check whether the graph is bipartite. Write the function like so:
template <typename T>
auto bipartite_check(const Graph<T>& G)
{
std::stack<size_t> stack;
std::set<size_t> visited;
stack.push(1); // Assume that BFS always starts from vertex ID 1
enum class colors {NONE, RED, BLUE};
colors current_color{colors::BLUE}; // This variable tracks the color to be assigned to the next vertex that is visited.
std::vector<colors> vertex_colors(G.vertices(), colors::NONE);
while (!stack.empty())
{
auto current_vertex = stack.top();
stack.pop();
// If the current vertex hasn't been visited in the past
if (visited.find(current_vertex) == visited.end())
{
visited.insert(current_vertex);
vertex_colors[current_vertex] = current_color;
if (current_color == colors::RED)
{
std::cout << "Coloring vertex " << current_vertex << " RED" << std::endl;
current_color = colors::BLUE;
}
else
{
std::cout << "Coloring vertex "
<< current_vertex << " BLUE" << std::endl;
current_color = colors::RED;
}
// Add unvisited adjacent vertices to the stack.
for (auto e : G.outgoing_edges(current_vertex))
if (visited.find(e.dest) == visited.end())
stack.push(e.dest);
}
// If the found vertex is already colored and
// has a color same as its parent's color, the graph is not bipartite
else if (visited.find(current_vertex) != visited.end() &&
((vertex_colors[current_vertex] == colors::BLUE &&
current_color == colors::RED) ||
(vertex_colors[current_vertex] == colors::RED &&
current_color == colors::BLUE)))
return false;
}
// If all vertices have been colored, the graph is bipartite
return true;
}
- Use the following functions to implement the test and driver code that tests our implementation of the bipartite checking algorithm:
template <typename T>
void test_bipartite()
{
// Create an instance of and print the graph
auto BG = create_bipartite_reference_graph<T>();
std::cout << BG << std::endl;
if (bipartite_check<T>(BG))
std::cout << "The graph is bipartite" << std::endl;
else
std::cout << "The graph is not bipartite" << std::endl;
}
int main()
{
using T = unsigned;
test_bipartite<T>();
return 0;
}
- Run the program. You should see the following output:

Figure 6.34: Output of Activity 13
Activity 14: Shortest Path in New York
In this activity, we will use the graph of various locations in New York City and find the shortest distance between the two given vertices. Follow these steps to complete the activity:
- Add the required header files and declare the graph, as shown here:
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <limits>
#include <queue>
#include <fstream>
#include <sstream>
template<typename T> class Graph;
- Implement the weighted edge that will be used in the graph:
template<typename T>
struct Edge
{
size_t src;
size_t dest;
T weight;
// To compare edges, only compare their weights,
// and not the source/destination vertices
inline bool operator< (const Edge<T>& e) const
{
return this->weight < e.weight;
}
inline bool operator> (const Edge<T>& e) const
{
return this->weight > e.weight;
}
};
- Overload the << operator for the Graph class so that it can be output to the C++ streams:
template <typename T>
std::ostream& operator<<(std::ostream& os, const Graph<T>& G)
{
for (auto i = 1; i < G.vertices(); i++)
{
os << i << ":\t";
auto edges = G.outgoing_edges(i);
for (auto& e : edges)
os << "{" << e.dest << ": " << e.weight << "}, ";
os << std::endl;
}
return os;
}
- Implement an edge list graph, as shown here:
template<typename T>
class Graph
{
public:
// Initialize the graph with N vertices
Graph(size_t N) : V(N)
{}
// Return number of vertices in the graph
auto vertices() const
{
return V;
}
// Return all edges in the graph
auto& edges() const
{
return edge_list;
}
void add_edge(Edge<T>&& e)
{
// Check if the source and destination vertices are within range
if (e.src >= 1 && e.src <= V &&
e.dest >= 1 && e.dest <= V)
edge_list.emplace_back(e);
else
std::cerr << "Vertex out of bounds" << std::endl;
}
// Returns all outgoing edges from vertex v
auto outgoing_edges(size_t v) const
{
std::vector<Edge<T>> edges_from_v;
for (auto& e : edge_list)
{
if (e.src == v)
edges_from_v.emplace_back(e);
}
return edges_from_v;
}
// Overloads the << operator so a graph be written directly to a stream
// Can be used as std::cout << obj << std::endl;
template <typename T>
friend std::ostream& operator<< <>(std::ostream& os, const Graph<T>& G);
private:
size_t V; // Stores number of vertices in graph
std::vector<Edge<T>> edge_list;
};
- Write the following function so that you can parse the graph file and prepare the graph:
template <typename T>
auto read_graph_from_file()
{
std::ifstream infile("USA-road-d.NY.gr");
size_t num_vertices, num_edges;
std::string line;
// Read the problem description line that starts with 'p' and looks like:
// p <num_vertices> <num_edges>
while (std::getline(infile, line))
{
if (line[0] == 'p')
{
std::istringstream iss(line);
char p;
std::string sp;
iss >> p >>sp >> num_vertices >> num_edges;
std::cout << "Num vertices: " << num_vertices
<< " Num edges: " << num_edges <<std::endl;
break;
}
}
Graph<T> G(num_vertices + 1);
// Read the edges and edge weights, which look like:
// a <source_vertex> <destination_vertex> <weight>
while (std::getline(infile, line))
{
if (line[0] == 'a')
{
std::istringstream iss(line);
char p;
size_t source_vertex, dest_vertex;
T weight;
iss >> p >> source_vertex >> dest_vertex >> weight;
G.add_edge(Edge<T>{source_vertex, dest_vertex, weight});
}
}
infile.close();
return G;
}
- Now, we need a struct that implements a Label struct that will be assigned to each vertex as Dijkstra's algorithm runs. Implement it as follows:
template<typename T>
struct Label
{
size_t vertex_ID;
T distance_from_source;
Label(size_t _id, T _distance) :
vertex_ID(_id),
distance_from_source(_distance)
{}
// To compare labels, only compare their distances from source
inline bool operator< (const Label<T>& l) const
{
return this->distance_from_source < l.distance_from_source;
}
inline bool operator> (const Label<T>& l) const
{
return this->distance_from_source > l.distance_from_source;
}
inline bool operator() (const Label<T>& l) const
{
return this > l;
}
};
- Dijkstra's algorithm can be implemented as follows:
template <typename T>
auto dijkstra_shortest_path(const Graph<T>& G, size_t src, size_t dest)
{
std::priority_queue<Label<T>, std::vector<Label<T>>, std::greater<Label<T>>> heap;
std::set<int> visited;
std::vector<size_t> parent(G.vertices());
std::vector<T> distance(G.vertices(), std::numeric_limits<T>::max());
std::vector<size_t> shortest_path;
heap.emplace(src, 0);
parent[src] = src;
// Search for the destination vertex in the graph
while (!heap.empty()) {
auto current_vertex = heap.top();
heap.pop();
// If the search has reached the destination vertex
if (current_vertex.vertex_ID == dest) {
std::cout << "Destination " <<
current_vertex.vertex_ID << " reached." << std::endl;
break;
}
if (visited.find(current_vertex.vertex_ID) == visited.end()) {
std::cout << "Settling vertex " <<
current_vertex.vertex_ID << std::endl;
// For each outgoing edge from the current vertex,
// create a label for the destination vertex and add it to the heap
for (auto e : G.outgoing_edges(current_vertex.vertex_ID)) {
auto neighbor_vertex_ID = e.dest;
auto new_distance_to_dest=current_vertex.distance_from_source
+ e.weight;
// Check if the new path to the destination vertex
// has a lower cost than any previous paths found to it, if // yes, then this path should be preferred
if (new_distance_to_dest < distance[neighbor_vertex_ID]) {
heap.emplace(neighbor_vertex_ID, new_distance_to_dest);
parent[e.dest] = current_vertex.vertex_ID;
distance[e.dest] = new_distance_to_dest;
}
}
visited.insert(current_vertex.vertex_ID);
}
}
// Construct the path from source to the destination by backtracking
// using the parent indexes
auto current_vertex = dest;
while (current_vertex != src) {
shortest_path.push_back(current_vertex);
current_vertex = parent[current_vertex];
}
shortest_path.push_back(src);
std::reverse(shortest_path.begin(), shortest_path.end());
return shortest_path;
}
- Finally, implement the test and driver code, as shown here:
template<typename T>
void test_dijkstra()
{
auto G = read_graph_from_file<T>();
//std::cout << G << std::endl;
auto shortest_path = dijkstra_shortest_path<T>(G, 913, 542);
std::cout << "The shortest path between 913 and 542 is:" << std::endl;
for (auto v : shortest_path)
std::cout << v << " ";
std::cout << std::endl;
}
int main()
{
using T = unsigned;
test_dijkstra<T>();
return 0;
}
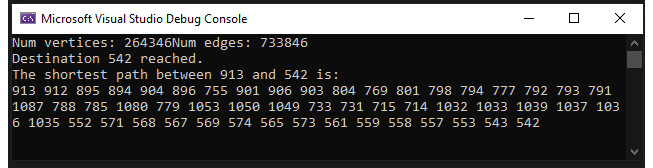
- Run the program. Your output should look as follows: