In Chapter 1, The Nuts and Bolts of Neural Networks, we discussed that many NN operations have solid mathematical foundations, and convolutions are no exception. Let's start by defining the mathematical convolution:
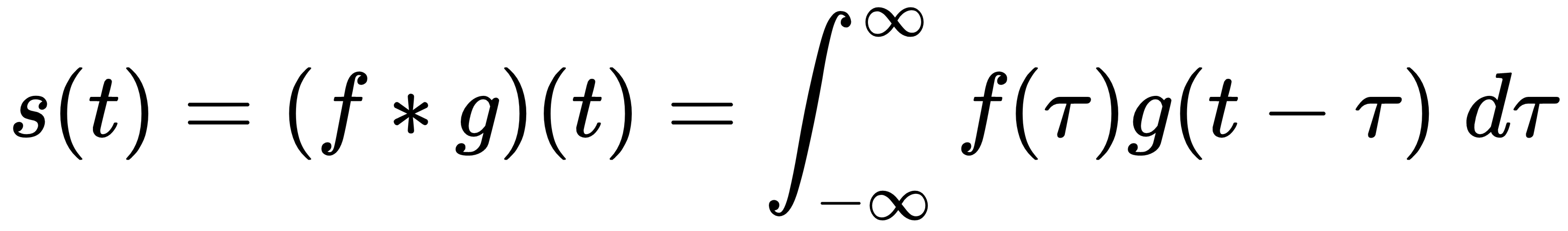
Here, we have the following:
- The convolution operation is denoted with *.
- f and g are two functions with a common parameter, t.
- The result of the convolution is a third function, s(t) (not just a single value).
The convolution of f and g at value t is the integral of the product of f(t) and the reversed (mirrored) and shifted value of g(t-τ), where t-τ represents the shift. That is, for a single value of f at time t, we shift g in the range 
and we compute the product f(t)g(t-τ) continuously because of the integral. The integral (and hence the convolution) is equivalent to the area under the curve of the product of the...
