Quantum expert Robert Sutor explains the basics of Quantum Computing

What if we could do chemistry inside a computer instead of in a test tube or beaker in the laboratory? What if running a new experiment was as simple as running an app and having it completed in a few seconds?

For this to really work, we would want it to happen with complete fidelity. The atoms and molecules as modeled in the computer should behave exactly like they do in the test tube. The chemical reactions that happen in the physical world would have precise computational analogs. We would need a completely accurate simulation.

If we could do this at scale, we might be able to compute the molecules we want and need.

These might be for new materials for shampoos or even alloys for cars and airplanes. Perhaps we could more efficiently discover medicines that are customized to your exact physiology. Maybe we could get a better insight into how proteins fold, thereby understanding their function, and possibly creating custom enzymes to positively change our body chemistry.

Is this plausible? We have massive supercomputers that can run all kinds of simulations. Can we model molecules in the above ways today?

This article is an excerpt from the book Dancing with Qubits written by Robert Sutor. Robert helps you understand how quantum computing works and delves into the math behind it with this quantum computing textbook.

Can supercomputers model chemical simulations?

Let’s start with C8H10N4O2 – 1,3,7-Trimethylxanthine.

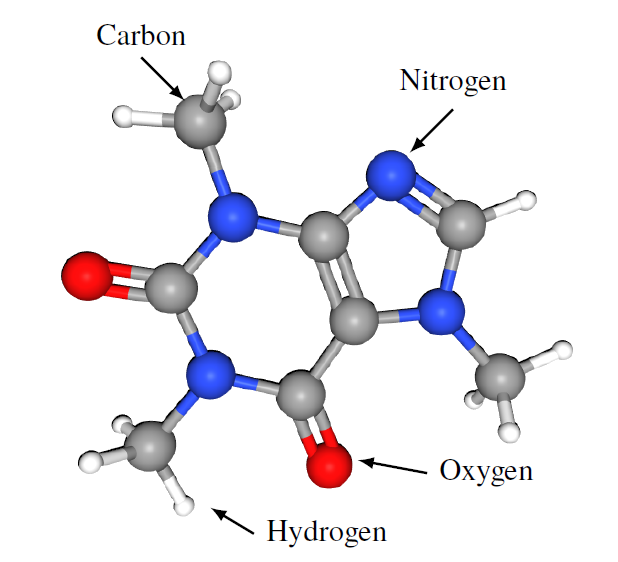
quantum-expert-robert-sutor-explains-the-basics-of-quantum-computing-img-0

This is a very fancy name for a molecule that millions of people around the world enjoy every day: caffeine. An 8-ounce cup of coffee contains approximately 95 mg of caffeine, and this translates to roughly 2.95 × 10^20 molecules. Written out, this is

295, 000, 000, 000, 000, 000, 000 molecules.

A 12 ounce can of a popular cola drink has 32 mg of caffeine, the diet version has 42 mg, and energy drinks often have about 77 mg.

These numbers are large because we are counting physical objects in our universe, which we know is very big. Scientists estimate, for example, that there are between 10^49 and 10^50 atoms in our planet alone.

To put these values in context, one thousand = 10^3, one million = 10^6, one billion = 10^9, and so on. A gigabyte of storage is one billion bytes, and a terabyte is 10^12 bytes.

Getting back to the question I posed at the beginning of this section, can we model caffeine exactly on a computer? We don’t have to model the huge number of caffeine molecules in a cup of coffee, but can we fully represent a single molecule at a single instant?

Caffeine is a small molecule and contains protons, neutrons, and electrons. In particular, if we just look at the energy configuration that determines the structure of the molecule and the bonds that hold it all together, the amount of information to describe this is staggering. In particular, the number of bits, the 0s and 1s, needed is approximately 10^48:

10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000.

And this is just one molecule! Yet somehow nature manages to deal quite effectively with all this information. It handles the single caffeine molecule, to all those in your coffee, tea, or soft drink, to every other molecule that makes up you and the world around you.

How does it do this? We don’t know! Of course, there are theories and these live at the intersection of physics and philosophy. However, we do not need to understand it fully to try to harness its capabilities.

We have no hope of providing enough traditional storage to hold this much information. Our dream of exact representation appears to be dashed. This is what Richard Feynman meant in his quote: “Nature isn’t classical.”

quantum-expert-robert-sutor-explains-the-basics-of-quantum-computing-img-1

However, 160 qubits (quantum bits) could hold 2^160 ≈ 1.46 × 10^48 bits while the qubits were involved in a computation. To be clear, I’m not saying how we would get all the data into those qubits and I’m also not saying how many more we would need to do something interesting with the information. It does give us hope, however.

In the classical case, we will never fully represent the caffeine molecule. In the future, with enough very high-quality qubits in a powerful quantum computing system, we may be able to perform chemistry on a computer.

How quantum computing is different than classical computing

I can write a little app on a classical computer that can simulate a coin flip. This might be for my phone or laptop.

Instead of heads or tails, let’s use 1 and 0. The routine, which I call R, starts with one of those values and randomly returns one or the other. That is, 50% of the time it returns 1 and 50% of the time it returns 0. We have no knowledge whatsoever of how R does what it does.

When you see “R,” think “random.” This is called a “fair flip.” It is not weighted to slightly prefer one result over the other. Whether we can produce a truly random result on a classical computer is another question. Let’s assume our app is fair.

If I apply R to 1, half the time I expect 1 and another half 0. The same is true if I apply R to 0. I’ll call these applications R(1) and R(0), respectively.

If I look at the result of R(1) or R(0), there is no way to tell if I started with 1 or 0. This is just like a secret coin flip where I can’t tell whether I began with heads or tails just by looking at how the coin has landed. By “secret coin flip,” I mean that someone else has flipped it and I can see the result, but I have no knowledge of the mechanics of the flip itself or the starting state of the coin.

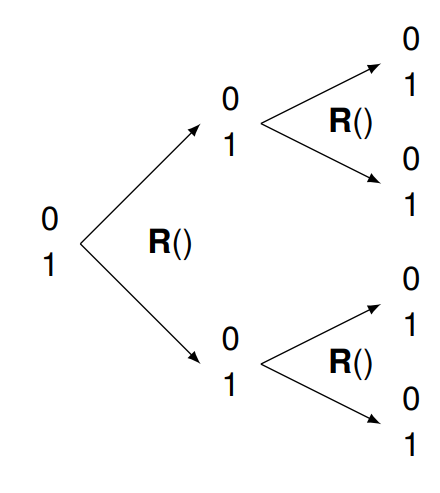
quantum-expert-robert-sutor-explains-the-basics-of-quantum-computing-img-2

If R(1) and R(0) are randomly 1 and 0, what happens when I apply R twice?

I write this as R(R(1)) and R(R(0)). It’s the same answer: random result with an equal split. The same thing happens no matter how many times we apply R. The result is random, and we can’t reverse things to learn the initial value.

Now for the quantum version, Instead of R, I use H. It too returns 0 or 1 with equal chance, but it has two interesting properties.

It is reversible. Though it produces a random 1 or 0 starting from either of them, we can always go back and see the value with which we began.

It is its own reverse (or inverse) operation. Applying it two times in a row is the same as having done nothing at all.

There is a catch, though. You are not allowed to look at the result of what H does if you want to reverse its effect. If you apply H to 0 or 1, peek at the result, and apply H again to that, it is the same as if you had used R. If you observe what is going on in the quantum case at the wrong time, you are right back at strictly classical behavior.

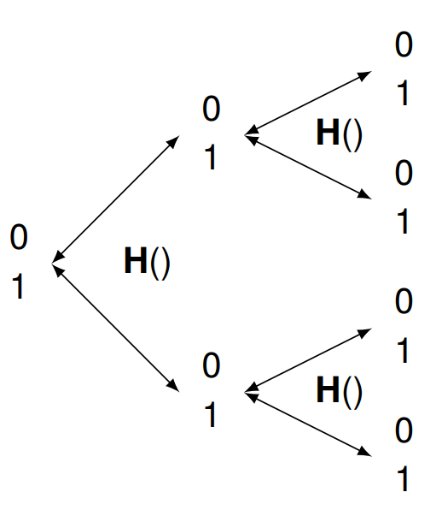
quantum-expert-robert-sutor-explains-the-basics-of-quantum-computing-img-3

To summarize using the coin language: if you flip a quantum coin and then don’t look at it, flipping it again will yield heads or tails with which you started. If you do look, you get classical randomness.

A second area where quantum is different is in how we can work with simultaneous values. Your phone or laptop uses bytes as individual units of memory or storage. That’s where we get phrases like “megabyte,” which means one million bytes of information.

A byte is further broken down into eight bits, which we’ve seen before. Each bit can be a 0 or 1. Doing the math, each byte can represent 2^8 = 256 different numbers composed of eight 0s or 1s, but it can only hold one value at a time. Eight qubits can represent all 256 values at the same time

This is through superposition, but also through entanglement, the way we can tightly tie together the behavior of two or more qubits. This is what gives us the (literally) exponential growth in the amount of working memory.

How quantum computing can help artificial intelligence

Artificial intelligence and one of its subsets, machine learning, are extremely broad collections of data-driven techniques and models. They are used to help find patterns in information, learn from the information, and automatically perform more “intelligently.” They also give humans help and insight that might have been difficult to get otherwise.

Here is a way to start thinking about how quantum computing might be applicable to large, complicated, computation-intensive systems of processes such as those found in AI and elsewhere. These three cases are in some sense the “small, medium, and large” ways quantum computing might complement classical techniques:

There is a single mathematical computation somewhere in the middle of a software component that might be sped up via a quantum algorithm.

There is a well-described component of a classical process that could be replaced with a quantum version.

There is a way to avoid the use of some classical components entirely in the traditional method because of quantum, or the entire classical algorithm can be replaced by a much faster or more effective quantum alternative.

As I write this, quantum computers are not “big data” machines. This means you cannot take millions of records of information and provide them as input to a quantum calculation. Instead, quantum may be able to help where the number of inputs is modest but the computations “blow up” as you start examining relationships or dependencies in the data.

In the future, however, quantum computers may be able to input, output, and process much more data. Even if it is just theoretical now, it makes sense to ask if there are quantum algorithms that can be useful in AI someday.

To summarize, we explored how quantum computing works and different applications of artificial intelligence in quantum computing.

Get this quantum computing book Dancing with Qubits by Robert Sutor today where he has explored the inner workings of quantum computing. The book entails some sophisticated mathematical exposition and is therefore best suited for those with a healthy interest in mathematics, physics, engineering, and computer science.