Understanding the three rules of topology
Now that we have a basic understanding of how a grid works, we can apply that understanding to a few more shapes. To do this, first, we need to understand the three conditions of good topology.
Rule 1 – an edge loop must terminate into the void or into itself
The first condition is that an edge loop needs to either terminate into the void or directly into itself. A cube is a perfect example of this. Like a plane, a default cube has the perfect topology for a cube. If you run a loop cut along any of the sides, all of the loops meet themselves all the way around. This is illustrated in Figure 2.12.
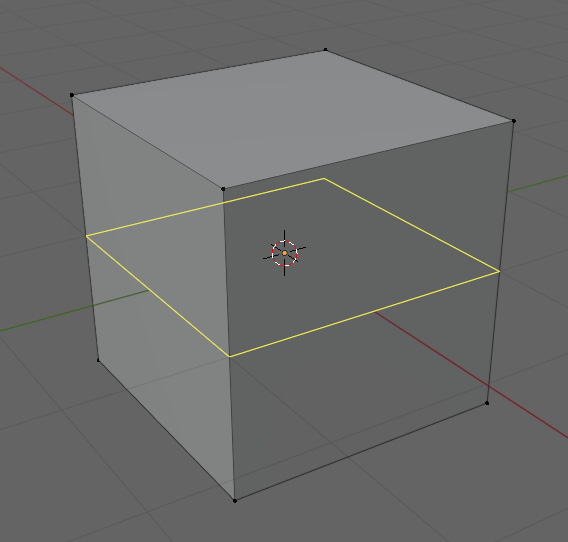
Figure 2.12 – Loop cut going around a cube
A cube is just six grids all joined end to end, with each grid having the same number of faces on them. If you were to isolate one of the sides, as in Figure 2.13, you would be able to run loops through it like any other grid. This is the core idea behind this...























































