Multivariate distributions
A multivariate probability distribution function is one that is induced by several variables. It is also called a joint probability function.
For a simple example, take the two (six-sided) dice experiment again. But this time, suppose that one die is red and the other is green. Let X be the number that comes up on the red die and Y be the number on the green die. These are two random variables, each ranging from 1 to 6. Their probability distribution is a function of those two variables:
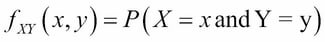
For example:
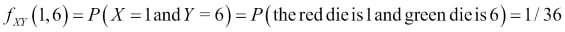
You can see that this probability is 1/36 from the fact that there are 36 possible outcomes and they are all equally likely (assuming the dice are balanced).
For a more interesting example, consider this experiment: a black bag contains two red marbles and four green marbles.
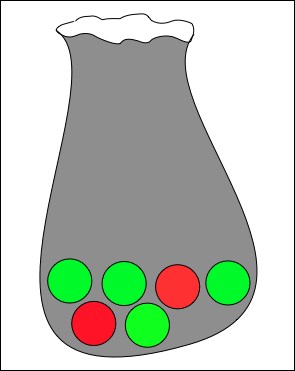
Figure 4-9. Bag of marbles
Except for their color, the marbles are identical. Two marbles are drawn at random from the bag, one after the other, without replacement. Let X be the number of red marbles...



































































