Aspects of functional programming
Functions can be simple or complex, but simpler functions are preferred. The function should ideally not change the state of memory or perform I/O, and consequently work with immutable data. These later two concepts are explored in Chapter 6, Optional and Monads.
There are several aspects of functional programming languages that we will explore here. They include:
- Functions
- Function composition
- Fluent interfaces
- Strict versus non-strict evaluation
- Parallelism
- Persistent data structures
- Recursion
- Optional and monads
Each of these concepts will be introduced in the following sections. We will explore the nature of each concept, explain why it is important, and when practical provide simple examples using Java.
Functions
Functions are the foundation of functional programming languages. They play a central role in supporting other functional programming concepts. In this section, we will introduce many of the terms used to describe functions including high-order, first-class, and pure functions. The concepts of closure and currying will also be explained.
First-class and high-order functions are associated with functional programming. A first-class function is a computer science term. It refers to functions that can be used anywhere a first-class entity can be used. A first-class entity includes elements such as numbers and strings. They can be used as an argument to a function, returned from a function, or assigned to a variable.
High-order functions depend upon the existence of first-class functions. They are functions that either:
- Take a function as an argument
- Return a function
Java 8 has introduced the concept of lambda expressions to the language. These are essentially anonymous functions that can be passed to and returned from functions. They can also be assigned to a variable. The basic form of a lambda expression follows where a parameter, such as x, is passed to the body of the function. The lambda operator, ->, separates the parameter from the body. This function is passed a value, which is multiplied by two and then returned, as follows:
x -> 2 * x
In this lambda expression, it is assumed that an integer is passed and that integer is returned. However, the data type is not restricted to an integer as we will see later. In the following lambda expression, an argument is passed and nothing is returned:
x->System.out.println(x)
Lambda expressions must be used in the proper context. It would not be appropriate to pass a lambda expression, which returns a value to a method, to a function that cannot use the returned value.
We can use the previous expression in many places that expect a single value being passed and nothing to be returned as shown next. In the following example, an array of integers is converted to a list. The lambda expression is then used as an argument to the List class's forEach method, which displays each element of the list. The forEach method applies the lambda expression to each element in the list, avoiding having to create an explicit loop to achieve the same effect:
Integer arr[] = {1,2,3,4,5};
List<Integer> list = Arrays.asList(arr);
list.forEach(x->System.out.println(x));Tip
Downloading the example code
You can download the example code files from your account at http://www.packtpub.com for all the Packt Publishing books you have purchased. If you purchased this book elsewhere, you can visit http://www.packtpub.com/support and register to have the files e-mailed directly to you.
The output will list the numbers one to five on separate lines.
Changing a program's state is avoided in functional programming. Calling a function with the same input values should result in the same behavior each time. This makes it easier to understand the function. Imperative programming changes the state using statements such as the assignment statement.
A pure function is a function that has no side effects. This means that memory external to the function is not modified, IO is not performed, and no exceptions are thrown. With a pure function, when it is called repeatedly with the same parameters, it will return the same value. This is called referential transparency.
With referential transparency, it is permissible to modify local variables within the function as this does not change the state of the program. Any changes are not seen outside of the function.
Advantages of pure function include:
- The function can be called repeatedly with the same argument and get the same results. This enables caching optimization (memorization).
- With no dependencies between multiple pure functions, they can be reordered and performed in parallel. They are essentially thread safe.
- Pure function enables lazy evaluation as discussed later in the Strict versus non-strict evaluation section. This implies that the execution of the function can be delayed and its results can be cached potentially improving the performance of a program.
- If the result of a function is not used, then it can be removed since it does not affect other operations.
There are several other terms associated with functions, such as the term closure. This refers to a function passed around along with its environment. The environment consists of the variables it uses. Java 8 supports a form of closure, and will be illustrated in Chapter 2, Putting the Function in Functional Programming.
Currying is the process of evaluating multiple arguments of a function one-by-one, producing intermediate results. In the process, we introduce a new function with one less argument than the previous step. For example, let's start with this function:
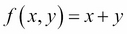
We can evaluate it for the value of 3 and 4 as follows, returning a result of 7:
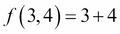
If we substitute 3 for x we get:
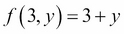
Next, if we define g(y) as:
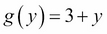
Then, the following is also true:
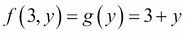
We reduced the number of arguments from two to one. Using a value of 4 for y yields the original result of 7. The process of currying, and partially applying functions, permit high-order functions to be used more effectively. This will become clearer in Chapter 2, Putting the Function in Functional Programming.
Function composition
Imperative programming places emphasis on a step-by-step process to implement an application. This is typified by a logical set of steps where code is executed using basic control constructs and is often encapsulated in functions or procedures.
Functional programming places more emphasis on how these functions are arranged and combined. It is this composition of functions, which typifies a functional style of programming. Functions are not only used to organize the execution process, but are also passed and returned from functions. Often data and the functions acting on the data are passed together promoting more capable and expressive programs.
We will illustrate this technique using the Function interface as defined in the java.util.function package. This interface possesses a compose and andThen methods. Both of these methods return a composed function.
The compose method will execute the function passed to it first, and then uses its result with the function the compose method is executed against. The andThen method will execute the first function and then execute the function passed as an argument to the andThen method.
The next code sequence demonstrates the compose method, which is passed as a function to take the absolute value of a number. The absThenNegate variable is assigned a function that will also negate the number. This variable is declared as a Function type, which means that the function assigned to it expects to be passed as an integer and returns an integer.
This function will execute the argument of the compose method and the Math class's abs method first, against some value, and then apply the negateExact method to this result. In other words, it will take the absolute value of a number and then negate it. Both of these methods are expressed as method references, which are new to Java 8. A method reference consist of the class name followed by a set of double colons, and then a method name providing a simpler form of method invocation:
Function<Integer,Integer>absThenNegate =
((Function<Integer,Integer>)Math::negateExact)
.compose(Math::abs);This is illustrated with the following sequence. The Function interface's apply method is used to invoke the composed function:
System.out.println(absThenNegate.apply(-25)); System.out.println(absThenNegate.apply(25));
Both of these statements will display a -25. In the first statement, the absolute value of a -25 is obtained and then negated. The second statement works the same way except its argument is +25.
The negateThenAbs variable that follows, illustrates the andThen method. The function used as an argument to the andThen method is applied after the first function is executed. In this case, the negateExact method is executed first and then the abs function is applied:
Function<Integer,Integer>negateThenAbs =
((Function<Integer,Integer>)Math::negateExact)
.andThen(Math::abs);
System.out.println(negateThenAbs.apply(-25));
System.out.println(negateThenAbs.apply(25));The output of both display statements will be 25.
We could have obtained the same results with a series of imperative statements. However, this does not result in as much flexibility as can be obtained using function composition. The ability to pass functions will provide the enhanced flexibility. We will postpone a detailed discussion of this approach until Chapter 3, Function Composition and Fluent Interfaces.
Fluent interfaces
Fluent interfaces constitute a way of composing expressions that are easier to write and understand. A fluent interface is often implemented using method chaining, sometimes called method cascading, where the returned value is used again in the same context.
In Java 8, the use of fluent interfaces is found in numerous places. We will illustrate this style with an example using the new Date and Time API.
Suppose we want to calculate a new date that is 2 years in the future, minus 1 month plus 3 days. We can use the following code sequence to achieve this result. The LocalDate class's method now returns an instance of the LocalDate class representing the current date. This date is the base for creating a new day called futureDate:
LocalDate today = LocalDate.now(); LocalDate futureDate = today.plusYears(2); futureDate = futureDate.minusMonths(1); futureDate = futureDate.plusDays(3); System.out.println(today); System.out.println(futureDate);
This will generate the following output:
2015-03-22 2017-02-25
Contrast this with the next code sequence, which takes advantage of the APIs fluent interface and produces the same output:
LocalDatefutureDate = LocalDate.now() .plusYears(2) .minusMonths(1) .plusDays(3);
The code flow is easy to read and flows in a more natural way. You will see repeated usage of fluent interfaces in the book. Streams use this approach consistently.
Strict versus non-strict evaluation
Functional languages can be classified as either using strict or non-strict evaluation of expressions. With strict evaluation, sometimes called eager evaluation, the expressions are evaluated as they are encountered.
With non-strict evaluation, they are not evaluated until necessary. Non-strict evaluation is sometimes called lazy evaluation. However, these terms are not always strict synonyms. Non-strict evaluation is concerned with the semantics of the expression, while lazy evaluation deals more with how the expression is evaluated.
Lazy evaluation is supported using streams. A stream can be thought of as a series of elements that flow like a river or stream. They add a convenient means of processing data in an easy-to-use and natural manner. The stream concept is support in Java 8 with the Stream class.
In the following sequence, a stream is created by generating five random numbers, sorting these numbers, and then displaying them:
Random random = new Random();
random.ints()
.limit(5)
.sorted()
.forEach(x->System.out.println(x));The ints method returns an IntStream instance. The limit method will restrict the stream to the first five numbers, and the sorted method will sort these numbers. However, the stream is not evaluated until a terminal method such as the forEach method is encountered. The use of streams will be demonstrated in more detail in Chapter 4, Streams and the Evaluation of Expressions.
One possible output follows:
-1790144043 -1777206416 23979263 801416357 874941096
A stream is processed lazily, which enables the runtime system to optimize how the stream's component operations are executed. In addition, they are used in a fluent manner.
Persistent data structures
Persistent data structures maintain previous versions of itself. As changes to the data structure occur, a new version of the data structure is created while maintaining the older version. These structures are effectively immutable.
Avoiding the mutation of data obviously has no side effects. This means that they are thread-safe and enable various optimization techniques.
One consequence of mutable data is that, when accessed from multiple threads, many threading issues arise that can make a program less reliable and maintainable. If the data is immutable, then these threading issues such as the need to synchronize data access largely go away.
One approach used by functional programming languages to simulate state is using a data structure, which is passed to a function. The data structure is copied and any changes made are reflected in the new copy of the data structure. This is referred to a state-passing style and can use a considerable amount of memory unless appropriate optimization techniques are applied.
There are immutable collections that support the concept of persistent data structures. However, when a language is entirely immutable, then a large amount of garbage is generated requiring extensive optimization to be useful. Some of these collections are not practical when they contain a significant number of elements.
We are not able to show how Java can support this concept here. However, in Chapter 6, Optional and Monads we will examine techniques that can be used in Java 8 to support data structures, such as some monads, in more detail.
Recursion
A loop is used in an imperative language to perform repeated calculations. Recursion is a technique that can achieve the same effect but often in a more elegant manner. A function is recursive if it calls itself either directly or indirectly. For example, calculating the factorial of a number can be accomplished using either iteration or recursion. The factorial of a number is defined as follows:
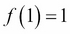
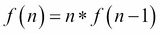
where n>0
An iterative solution follows:
int result = 1;
for (int i = 5; i>= 1; i--) {
result = result * i;
}
System.out.println(result);The output will be 120. The equivalent recursion solution starts with a recursive factorial function:
public int factorial(int n) {
if(n==1) {
return 1;
} else {
return n * factorial(n-1);
}
}This solution is more succinct than the iterative version and more closely matches the problem definition. The function can be invoked as follows:
System.out.println(factorial(num));
It will generate the same output: 120.
Indirect recursion occurs when a function calls itself but not immediately. For example, if function A calls function B, which then calls function A, we have indirect recursion.
A recursion function needs to be bounded. This means that it must stop calling itself at some time. Otherwise, it will exceed the system's resources and result in an exception being thrown and the program terminating abnormally. In the factorial function, the test for an n value of 1 stopped the recursion.
Frequently, recursion is implemented using a program stack. However, if tail recursion is used, then the compiler can avoid the use of a program stack and use essentially the same technique used to implement an imperative loop. Tail recursion involves a tail call, which is where the recursive call is the last statement of the function.
Parallelism
One area where the use of functional programming can be useful is handling parallel, also called concurrent, programming tasks. Consider the following sequence:
result = a.methodA() + b.methodB() + c.methodC();
In what order can these methods be executed? If they have side effects, then they will most likely need to be computed sequentially. For example, the effect of methodA may affect the results of the other methods. However, if they do not have side effects, then the order of execution is not important and can be executed concurrently. Conceivably, they might not be executed at all until the value of result is needed, if ever. This is another potential application of lazy evaluation.
Java has steadily improved its support of concurrent programming over the years. These approaches built upon the underlying Thread class and provided various classes to support specific concurrent task such as pools.
The problem with these earlier approaches has been the need to learn these models and decide if they are a good fit for the problem at hand. While this is necessary and works well for many problem areas, it does require more effort on the part of the developer to learn these techniques.
In Java 8, much of the effort requires to add concurrent behavior to a program has been lessened allowing the developer to focus more on the problem at hand. This support comes in the use of functions in conjunction with streams and collections.
For example, the next code sequence illustrates how a lambda expression can be applied to each member of a stream. The Stream class's of method will generate a stream of integers. The map function applies the lambda expression, x->x*2, to each element of the stream:
Stream<Integer> stream = Stream.of(12, 52, 32, 74, 25);
stream.map(x->x*2)
.forEach(x ->System.out.println(x));The output follows:
24 104 64 148 50
This can be parallelized easily using the parallel method as shown here:
stream = Stream.of(12, 52, 32, 74, 25);
stream.parallel().map(x->x*2)
.forEach(x ->System.out.println(x));One possible output follows. However, since the stream operations are executed in parallel, a different output ordering is possible:
64 148 50 104 24
When the lambda expression is executed concurrently on different elements of the stream, the operations can be assigned to different processors and at different times. There is no guarantee with regard to the order in which the operations will be executed.
Humans are not very adept at multitasking, let alone writing concurrent programs that are reliable. By moving some of the decision-making process to the compiler and runtime system, more capable and efficient programs can be created.
Optional and monads
Null pointer exceptions are common, and their very existence is problematic to many developers. They introduce a slew of problems, including the need to handle them gracefully. The Optional class has been introduced in Java 8 to help deal with null pointer exceptions. It helps preserve type safety. The approach will ease the use of functions, provide an opportunity for using fluent interfaces, and avoid exception handling boilerplate code.
The intent of the Optional class is to help programmers deal with situations where a failure may occur. One way of handling this type of problem has been to return a null reference indicating a missing value. Using the Optional class forces the programmer to explicitly deal with the possibility that a function might not return a value. The Optional type should be used as the return type of a method or function that might not return a value.
Consider the situation where we would like to return an instance of a Customer class based on an ID using the following method:
public Optional<Customer>findCustomerWithID(long id) {
//...
return someValue;
}Later when we invoke the function, a value of the Optional<Customer> type will be returned. We need to use the isPresent method to explicitly determine if a value is returned. If it is present, then the get method returns the actual Customer instance as shown next:
Optional<Customer>optionalCustomer = findCustomerWithID(123);
if (optionalCustomer.isPresent()) {
Customer customer = optionalCustomer.get();
// Use customer
} else {
// handle missing value
}The problem with simply returning null is that the programmer may not realize that a method may return null and may not attempt to handle it. This will result in a null pointer exception. In this example, since the findCustomerWithID method explicitly used the Optional type, we know and must deal with the possibility that nothing may be returned.
The Optional type allows chained function calls where a method might not return a value. We will demonstrate this in Chapter 6, Optional and Monads where the Optional type is discussed in more detail.
The Optional type has a monadic structure. A monad is basically a structure containing a set of computations represented as a series of steps. These computations are chained together effectively forming a pipeline. However, there is more to monads than this. Monads are a very useful technique and promote more reliable programs than most imperative programming techniques are capable of doing. You will learn more about the nature of monads and how to use them in Chapter 6, Optional and Monads.
In the same way, as you need to choose the right hammer for a job, you also need to choose the right language and programming style for the programming task. We don't want to use a sledge hammer to put a small nail in the wall for a picture. Since most jobs consist of multiple tasks, we need to use the right programming style for the specific task at hand.
Hence, a major focus of the book is how to blend the various programming styles available in Java 8 to meet an application's need. To be able to decide which technique is best for a given job, one needs to understand the nature of the task and how a technique supports such a task.
The incorporation of these functional programming techniques does not make Java a functional programming language. It means that we now have a new set of tools that we can use to solve the programming problems presented to us. It behooves us to take advantage of these techniques whenever they are applicable.























































