5.9 Change of basis
Given an n-dimensional vector space V, we can choose different bases for V. Let’s call two of them basis$change of
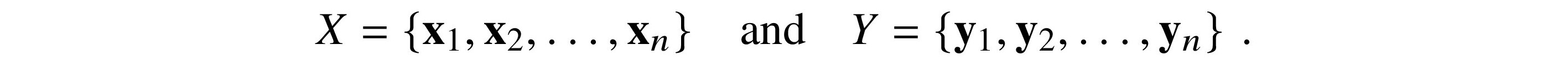
If v is a vector in V, it has one set of coordinates corresponding to X and another set for Y. How do we change from one set of coordinates for v to the other?
Let’s look at an example demonstrating how the choice of basis can make things easier.
Suppose we have city blocks laid out in a rectilinear pattern as in Figure 5.20. We use the basis vectors x1 = (1, 0) and x2 = (0, 2) to position ourselves. I’ve given the coordinates using the standard basis.
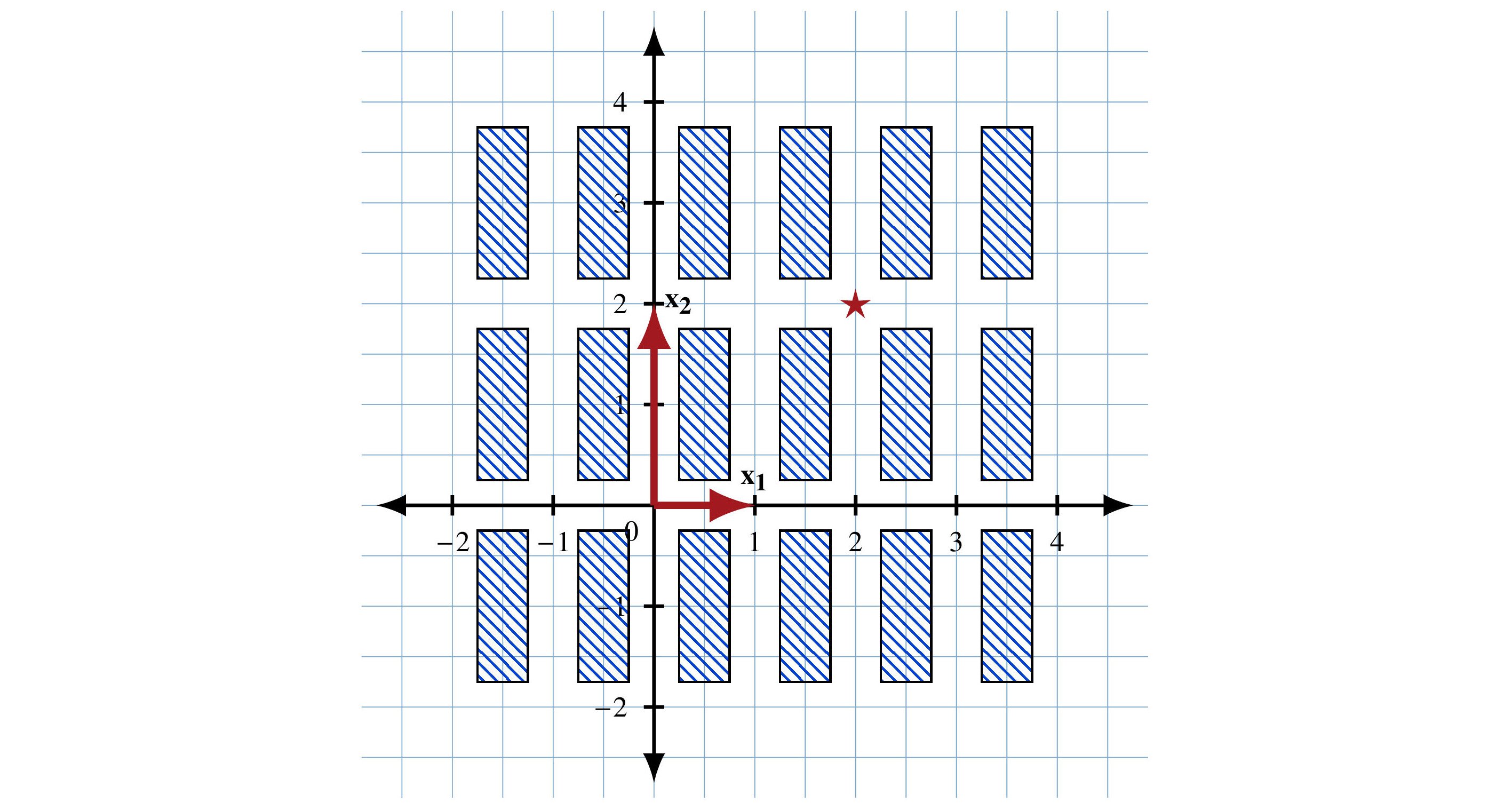
I can give you directions by saying, “Go north along x2 for 1 block, turn right, and go east along x1 for 2 blocks.” That puts you where the star is in the picture. In terms of the X basis, the position is 2x1 +...
































































