The Eggholder function, depicted in the following diagram, is often used as a benchmark for function optimization algorithms. Finding the single global minimum of this function is considered a difficult task due to the large number of local minima, which give it the eggholder shape:
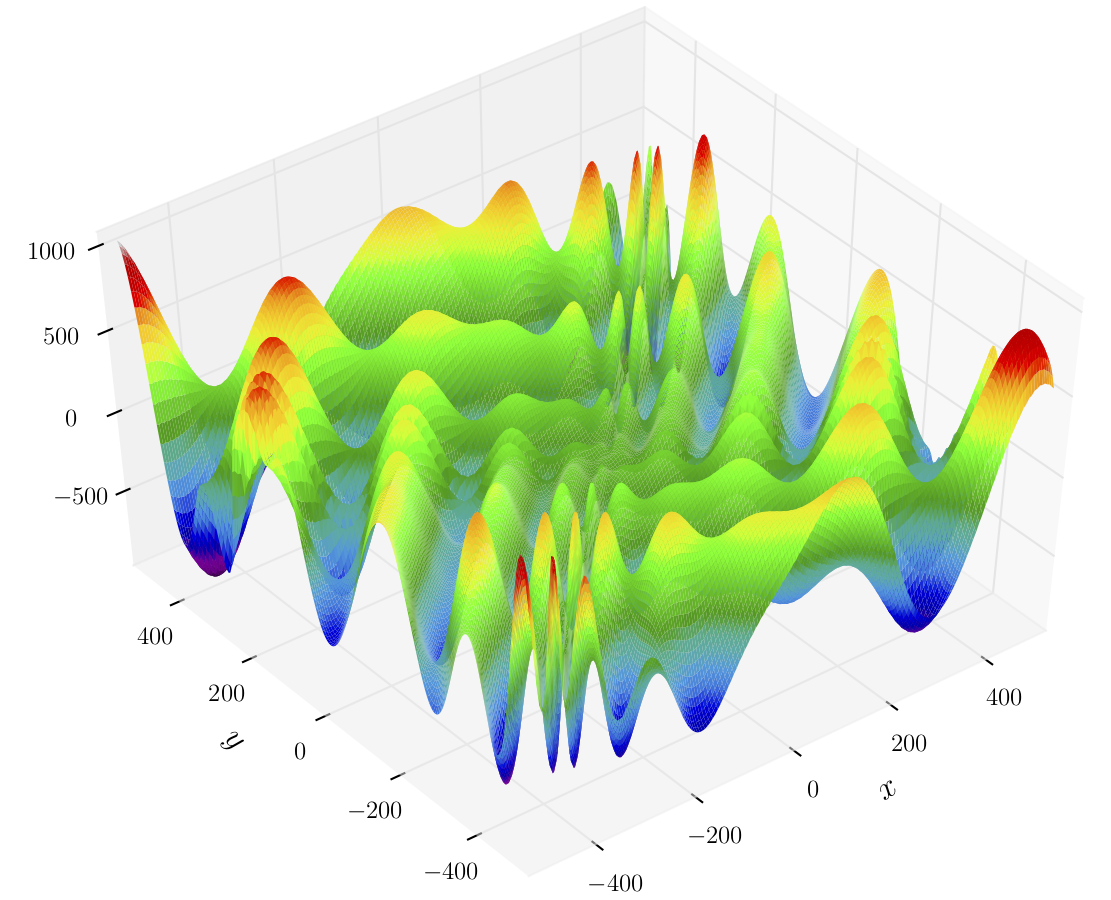
The Eggholder function
Source: https://en.wikipedia.org/wiki/File:Eggholder_function.pdf. Image by Gaortizg.
Licensed under Creative Commons CC BY-SA 3.0: https://creativecommons.org/licenses/by-sa/3.0/deed.en.
Source: https://en.wikipedia.org/wiki/File:Eggholder_function.pdf. Image by Gaortizg.
Licensed under Creative Commons CC BY-SA 3.0: https://creativecommons.org/licenses/by-sa/3.0/deed.en.
The function can be mathematically expressed as follows:
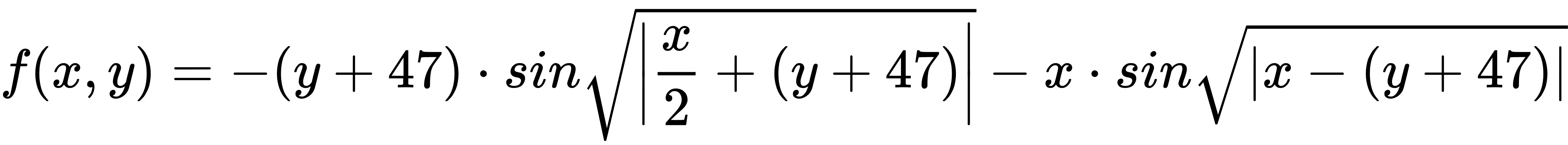
It is usually evaluated on the search space bounded by [-512, 512] in each dimension.
The global minimum of the function is known to be at:
x=512, y = 404.2319
Where the function's value is -959.6407.
In the next subsection, we will attempt to find the global minimum using the genetic algorithms...

































































