Spatial data are references for an object's position on the Earth's surface. How can you measure and store them in a numeric format? An elementary model of the Earth could be a sphere. On a sphere's surface, you can measure positions with angular units called latitude (ϕ) and longitude (λ). Latitude measures the angle between the equatorial plane and a line that passes through that point, and is normal to the surface; whereas, longitude measures the east or west angle from a reference meridian (for example, the one passing through Greenwich observatory) to another meridian that passes through that point. Angular measures can be expressed in decimal degrees or in degrees, minutes, and seconds.
If you want to store the location of the Statue of Liberty, you can express it in the decimal degree form, as shown here:
40.689167, -74.044444
Alternatively, you can use the degrees, minutes, and seconds form as follows:
Lat. 40° 41′ 21″ N, Long. 74° 2′ 40″ W
Consider the image of the model of the Earth given as follows:
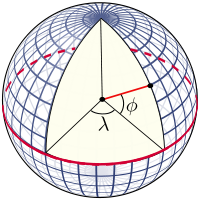
We normally think of the Earth as a sphere, but this is not its real shape. Geodesy, the science studying the shape of the Earth, defines the Earth, as represented by a geoid, an ideal surface defined by the level of the sea if oceans were to cover all of Earth. For practical purposes, as in projections, the geoid is too complicated to use, and so the Earth is defined by an ellipsoid. The ellipsoid is described by its semi-major axis (equatorial radius) and flattening.
































































