Magnitude
The magnitude or length of a vector is written as the letter of the vector surrounded by two bars,  . The magnitude of a vector is the square root of the dot product of the vector with itself:
. The magnitude of a vector is the square root of the dot product of the vector with itself:
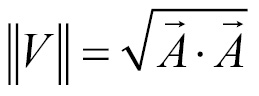
In addition to implementing the magnitude function, we're also going to implement a magnitude squared function. The formula is the same, but it avoids the expensive square root operation:
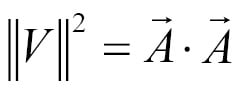
In games we often compare the magnitude of a vector to known numbers; however, doing a comparison between a number and the magnitude is expensive because of the square root operation. A simple solution to this problem is to square the number, and then compare against square magnitude. This means, instead of the following:
if (Magnitude(someVector) < 5.0f) {We could instead write the following:
if (MagnitudeSq(someVector) < 5.0f * 5.0f) {We'd then get the same result, avoiding the expensive square root operation.
Getting ready
To find the magnitude of a vector, take the square root of the vector's dot product with its-self. The square root operation is a relatively expensive one that should be avoided whenever possible. For this reason, we are also going to implement a function to find the square magnitude of a vector.
How to do it…
Follow these steps to implement a function for finding the length and squared length of two and three dimensional vectors.
- Add the declaration for magnitude and magnitude squared to
vectors.h:float Magnitude(const vec2& v); float Magnitude(const vec3& v); float MagnitudeSq(const vec2& v); float MagnitudeSq(const vec3& v);
- Add the implementation for these functions to
vectors.cpp:float Magnitude(const vec2& v) { return sqrtf(Dot(v, v)); } float Magnitude(const vec3& v) { return sqrtf(Dot(v, v)); } float MagnitudeSq(const vec2& v) { return Dot(v, v); } float MagnitudeSq(const vec3& v) { return Dot(v, v); }
How it works…
We can derive the equation for the magnitude of a vector from the geometric definition of the dot product that we briefly looked at in the last section:

Because we are taking the dot product of the vector with itself, we know the test vectors point in the same direction; they are co-directional. Because the vectors being tested are co-directional, the angle between them is 0. The cosine of 0 is 1, meaning the  part of the equation can be eliminated, leaving us with the following:
part of the equation can be eliminated, leaving us with the following:
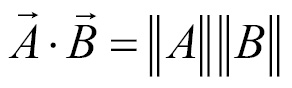
If both the test vectors are the same (which in our case they are) the equation can be written using only  :
:
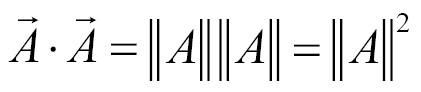
We can rewrite the preceding equation, taking the square root of both sides to find the length of vector  :
:
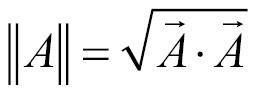
There's more…
The magnitude of a vector can be used to find the distance between two points. Assuming we have points  and
and  , we can find a vector (
, we can find a vector ( ) that connects them by subtracting
) that connects them by subtracting  from
from  , as shown in the following diagram:
, as shown in the following diagram:
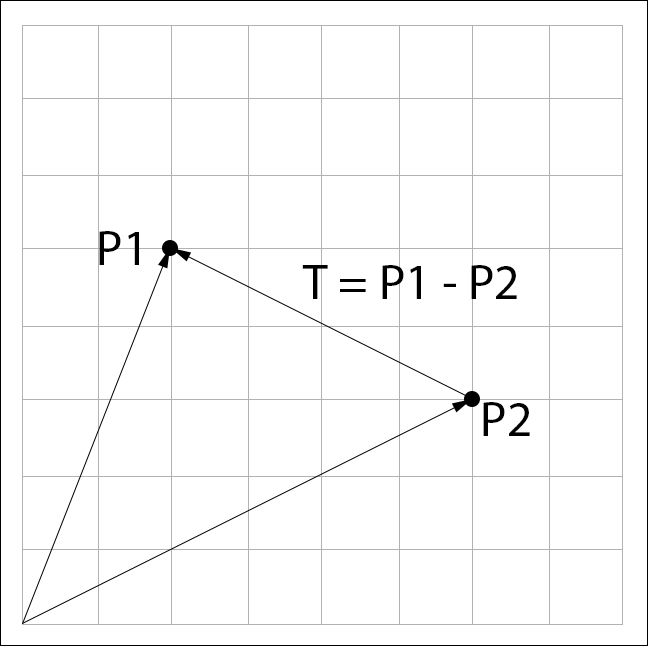
The distance between the two points is the length of  . This could be expressed in code as follows:
. This could be expressed in code as follows:
float Distance(const vec3& p1, const vec3& p2) {
vec3 t = p1 - p2;
return Magnitude(t);
}



























































