Importance sampling

Importance sampling is an improvement on rejection sampling. Again the assumptions are the same and we will use a proposal distribution q(x). We also assume that we can compute the value of the density of probability p(x). But we are unable to draw a sample from it because it is, again, too complex.

Importance sampling is based on the following reasoning, where we need to evaluate the expectation of a function f(x) with respect to the distribution p(x):

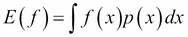
At this stage, we simply introduce the distribution q(x) in the previous expression:

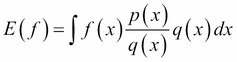
And, as before, we approximate it with a finite sum:

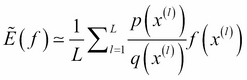
The ratio is called importance weight and it is the bias introduced by sampling q(x) when in fact we wanted to sample from p(x). In this case, the algorithm is very simple because all the samples are used. Again, importance sampling is efficient if the proposal distribution is close enough to the original distribution. If the function f(x) varies a lot, we might end up in a situation where...