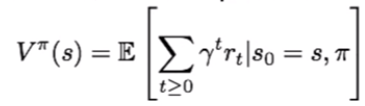First, we need to estimate the value (V) of state (s) while following a specific policy (π). This tells you the expected cumulative reward at the terminal state of a game while following a policy (π) starting at state (s). Why is this useful? Well, imagine that our learning agent's environment is populated by enemies that are continuously chasing the agent. It may have developed a policy dictating it to never stop running during the whole game. In this case, the agent should have enough flexibility to evaluate the value of game states (when it runs up to the edge of a cliff, for example, so as to not run off it and die). We can do this by defining the value function at a given state, V π (s), as the expected cumulative (discounted) reward that the agent receives from following that policy, starting from the current state: