Examples for Linear Algebra Methods in SymPy
The basic task in linear algebra is to solve linear equation systems:
 .
.
Let us do this symbolically for a 3 × 3 matrix:
A = Matrix(3,3,symbols('A1:4(1:4)'))
b = Matrix(3,1,symbols('b1:4'))
x = A.LUsolve(b)
The output of this relatively small problem is already merely readable which can be seen in the following expression:

Again, the use of simplify command helps us to detect canceling terms and to collect common factors:
simplify(x)
which will result in the following output which looks much better:
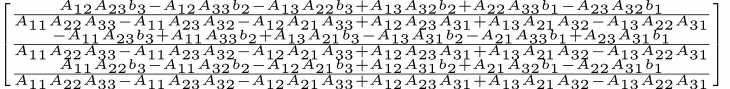
Symbolic computations becomes very slow with increase in matrix dimensions. For dimensions bigger than 15, there might even occur memory problems.
The preceding figure (Figure 15.3) illustrates the differences in CPU time between symbolically and numerically solving a linear system:
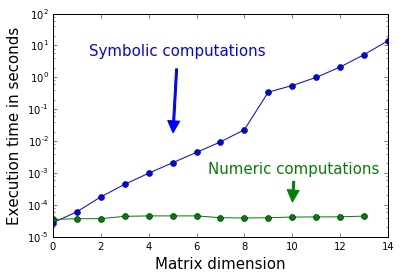
Figure 15.3: CPU time for numerically and symbolically solving a linear system.























































