Log-likelihood ratios recommendation system method
The log-likelihood ratio (LLR) is a measure of how two events A and B are unlikely to be independent but occur together more than by chance (more than the single event frequency). In other words, the LLR indicates where a significant co-occurrence might exist between two events A and B with a frequency higher than a normal distribution (over the two events variables) would predict.
It has been shown by Ted Dunning (http://tdunning.blogspot.it/2008/03/surprise-and-coincidence.html) that the LLR can be expressed based on binomial distributions for events A and B using a matrix k with the following entries:
|
A |
Not A | |
|---|---|---|
|
B |
k11 |
k12 |
|
Not B |
k21 |
k22 |
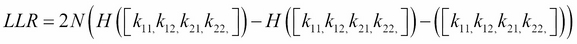
Here,  and
and  is the Shannon entropy that measures the information contained in the vector p.
is the Shannon entropy that measures the information contained in the vector p.
Note:  is also called the Mutual Information (MI) of the two event variables A and B, measuring how the occurrence of the two events depend on each other.
is also called the Mutual Information (MI) of the two event variables A and B, measuring how the occurrence of the two events depend on each other.
This test is also called G2, and it has been proven effective...
































































