Bayesian treatment of neural networks
To set the neural network learning in a Bayesian context, consider the error function  for the regression case. It can be treated as a Gaussian noise term for observing the given dataset conditioned on the weights w. This is precisely the likelihood function that can be written as follows:
for the regression case. It can be treated as a Gaussian noise term for observing the given dataset conditioned on the weights w. This is precisely the likelihood function that can be written as follows:

Here,  is the variance of the noise term given by
is the variance of the noise term given by 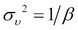 and
and 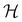 represents a probabilistic model. The regularization term can be considered as the log of the prior probability distribution over the parameters:
represents a probabilistic model. The regularization term can be considered as the log of the prior probability distribution over the parameters:

Here, 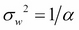 is the variance of the prior distribution of weights. It can be easily shown using Bayes' theorem that the objective function M(w) then corresponds to the posterior distribution of parameters w:
is the variance of the prior distribution of weights. It can be easily shown using Bayes' theorem that the objective function M(w) then corresponds to the posterior distribution of parameters w:

In the neural network case, we are interested in the local maxima of  . The posterior is then approximated as a Gaussian around each maxima
. The posterior is then approximated as a Gaussian around each maxima  , as follows:
, as follows:

Here, A is a matrix of the second derivative of M(w) with respect to w and represents an inverse of the covariance matrix...
































































