Solving partial differential equations with generative modeling
Another field in which deep learning in general, and generative learning in particular, have led to recent breakthroughs is the solution of partial differential equations (PDEs), a kind of mathematical model used for diverse applications including fluid dynamics, weather prediction, and understanding the behavior of physical systems. More formally, a PDE imposes some condition on the partial derivatives of a function, and the problem is to find a function that fulfills this condition. Usually some set of initial or boundary conditions is placed on the function to limit the search space within a particular grid. As an example, consider Burger's equation,8 which governs phenomena such as the speed of a fluid at a given position and time (Figure 13.8):
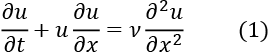
Where u is speed, t is time, x is a positional coordinate, and  is the viscosity ("oiliness") of the fluid. If the viscosity is 0, this simplifies...
is the viscosity ("oiliness") of the fluid. If the viscosity is 0, this simplifies...


























































