The question you may ask at this point is "Why should I care about graphs? After all, my company/business/interest is not about graphs or networks of any kind. I know my data model, well arranged into SQL tables or NoSQL documents, and I can retrieve the information I want when I want." This book will teach you how to empower your data by looking at it in a different way. Surprisingly enough, graphs can be used to model a lot of processes, from the more obvious ones such as road networks, to less intuitive use cases such as video games or credit card fraud detection, among many others.
Graph theory
Let's start from the beginning and answer the question "What is a graph?"
A bit of history: the Seven Bridges of Königsberg problem
Graph studies originate back to Leonhard Euler, a prolific Swiss mathematician who lived in the eighteenth century. In 1735, he published a paper proposing a solution to the Seven Bridges of Königsberg problem. The problem is the following:
Given the city whose geography is depicted in the following image, is there a way to walk across each of the seven bridges of the city once and only once, and return to our starting point?
As you can see, this city is crossed by a river that splits the city into two banks, A and B. The river meander additionally creates two islands, C and D, also part of the city. Those two banks and two islands are connected by a total of seven bridges: two bridges between A and C, two other bridges between C and B, one between C and D, one between B and D, and a last one between D and A:

Euler's reasoning (on the right side) was to reduce this complex geography to the most simple drawing, like the one you can see on the right of the previous image, since the route used within each island is not relevant. Each island then becomes a single point, or node, connected to another by one or several links, or edges, representing the bridges.
With this simple visualization, the mathematician was able to solve the initial problem by noting that, if you arrive at an island (vertex) via one bridge, you will need to leave it using another bridge (except for the start and end vertices). In other words, all vertices but two need to be connected to an even number of relationships. This is not the case in the Königsberg graph, since we have the following:
A: 3 connections (to C twice, and to D once)
B: 3 connections (to C twice, and to D once)
C: 5 connections (to A twice, to B twice and to D once)
D: 3 connections (to A once, to C once and to D once)
This kind of path, where each edge is used once and only once, is called a Eulerian cycle and it can be said that a graph has a Eulerian cycle if and only if all of its vertices have even degrees.
Graph definition
This leads us to the mathematical definition of a graph:
A graph G = (V, E) is a pair of:
- V, a set of nodes or vertices: the islands in our previous example
- E, a set of edges connecting nodes: the bridges
The Königsberg graph illustrated on the right of the preceding image can then be defined as follows:
V = [A, B, C, D]
E = [
(A, C),
(A, C),
(C, B),
(C, B),
(A, D),
(C, D),
(B, D)
]
Graphs, like many mathematical objects, are well defined. While it can be difficult to find a good visualization for some of those objects, graphs, on the other hand, suffer from the almost infinite number of ways to draw them.
Visualization
Apart from very special cases, there is no single way to draw a graph and visualize it. Indeed, graphs are most often an abstract representation of reality. For instance, all four graphs depicted in the following image represent the exact same set of nodes and edges, so, by definition, the same mathematical graph:

We cannot rely only on our eyes to find patterns within graphs. For instance, looking only at the lower-right plot, it would be impossible to see the pattern that is visible in the upper-right plot. That's where graph algorithms enter into the game, which will be discussed in more detail in Chapter 6, Node Importance, and Chapter 7, Community Detection and Similarity Measures.
Examples of graphs
Now that we have a better idea of what a graph is, it's time to discover some more examples to understand which purposes graphs can be useful for.
Networks
With the graph definition in mind (a set of nodes connected to each other via edges) and the bridges example from the last section, we can easily imagine how all kinds of networks can be seen as graphs, including road networks, computer networks, or even social networks.
Road networks
Road networks are a perfect example of graphs. In such networks, the nodes are the road intersections, and edges are the roads themselves, as you can see in the following image:

This image shows the road network around Central Park in New York City, wherein streets are edges between junctions representing nodes
With road networks, many questions can be answered with graph analysis, such as the following:
- What is the shortest path between two points (nodes)?
- How long is this shortest path?
- Are there alternative routes?
- How can you visit all nodes within a list in a minimal amount of time?
This last question is especially important for parcel delivery, in order to minimize the number of driven miles to maximize the number of delivered parcels and satisfied customers.
We will go into more detail about this topic in Chapter 4, The Graph Data Science Library and Path Finding.
Computer networks
In a computer network, each computer/router is a node and the cables between them are the edges. The following image illustrates some possible topologies used for a computer network (credit: https://commons.wikimedia.org/wiki/File:NetworkTopologies.svg):
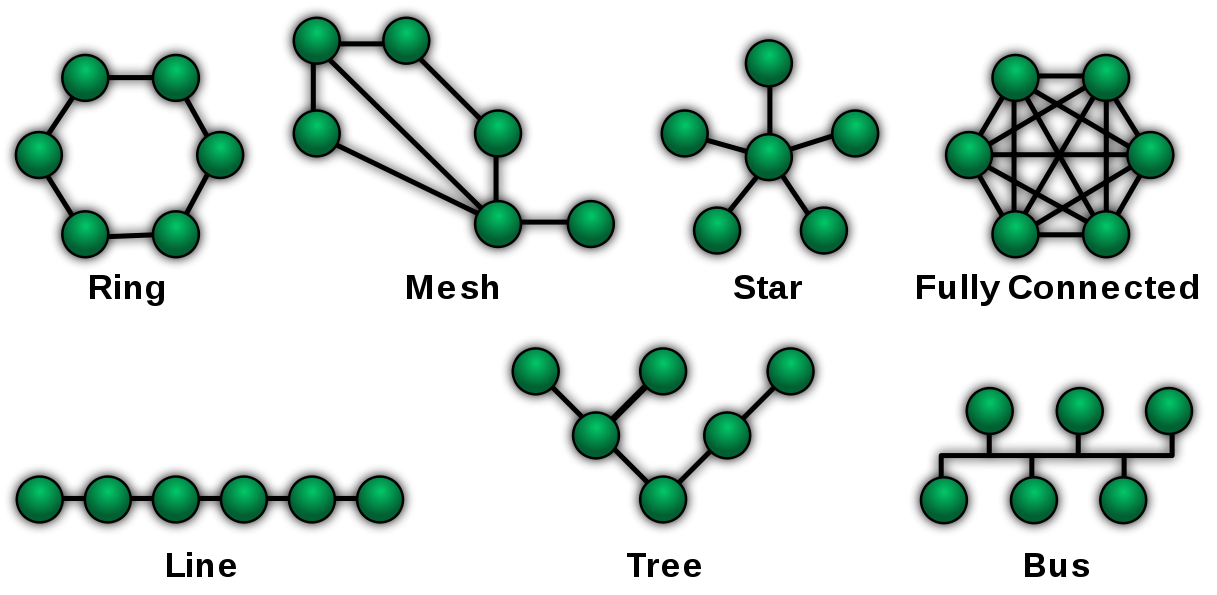
You can now draw the parallel with the graph definition we discovered in the last section. Here again, the graph structure helps in answering some common questions you may ask yourself about your network:
- How fast will this information be transferred from A to B? This sounds like a shortest path issue.
- Which of my nodes is the most critical one? By critical, we mean that if this node is not working for some reason, the whole network will be impacted. Not all nodes have the same impact on the network. That's where centrality algorithms come into the game (see Chapter 6, Node Importance).
Social networks
Facebook, LinkedIn, and all of our favorite social networks use graphs to model their users and interactions. In the most basic example of a social graph, nodes represent people, and edges the friendship or professional relationship between them, as illustrated in the following image:
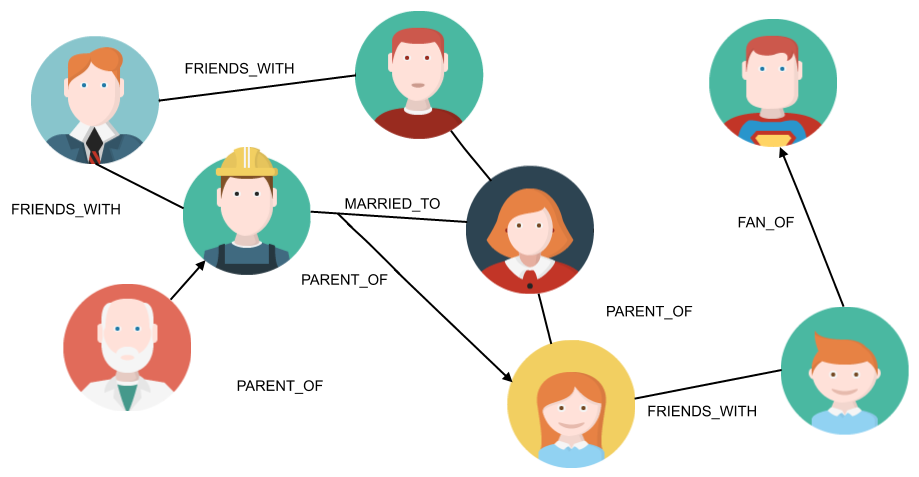
Here again, graphs allow us to see the data from a different perspective. For instance, we have seen this kind of information when looking at someone’s profile on LinkedIn:
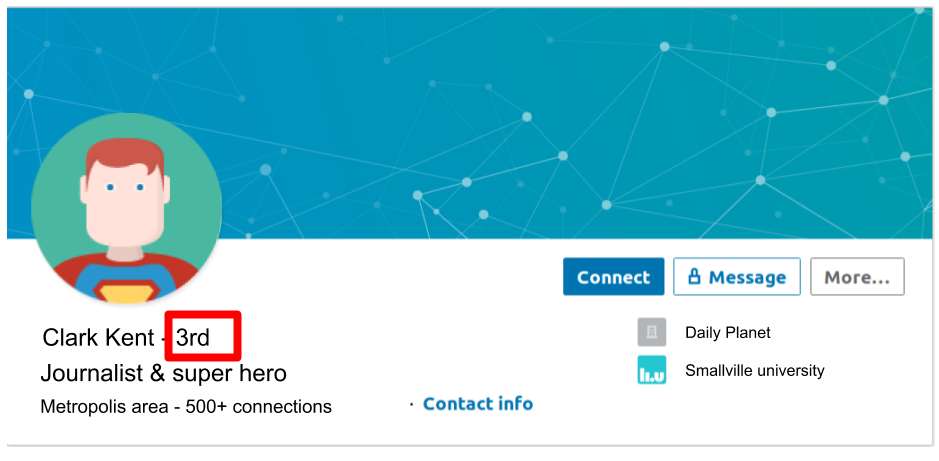
In that case, it tells us that the connected user (me) is just two connections away from Clark Kent. In other words, one person in my network is already connected to a person who is connected to Clark Kent. The following image illustrates this more clearly, in terms of degrees of separation:

You've probably heard about the Six Degrees of Separation theory. In 1929, the Hungarian journalist Frigyes Karinthy proposed a theory according to which each person on Earth is at most six connections away from any other person. In other words, if you want to talk to one person, say Barack Obama, a friend of yours has a friend whose friend has a friend... who knows Barack Obama and can introduce you to him. According to Karinthy, this connection chain must contain less than six connections, or seven people in total, including you and Barack Obama.
Given that there are more than 7 billion human beings on Earth, that's a surprisingly small number! With the large databases that are available nowadays, such as the friendship connections from Facebook or email exchanges from Microsoft, researchers have tried to prove the preceding statement. From the Microsoft email database, for instance, it was shown in 2008 that the average degree of separation between 180 billion distinct pairs of people was around 6.6. But this is just an average, and the number of hops to connect two people could go up to 29 with that dataset.
Many other kinds of analyses can be performed over social graphs:
- Node importance: Again, it might be very useful to have an idea of which nodes (persons) are the most important. However, the definition of importance here will be different than in the case of a computer network, since it is very unlikely that a single person's retirement from social media makes the whole world collapse. However, influencers have a particular interest for marketing experts.
- Community detection: Also called clustering, is a way to find a group of nodes sharing some characteristics. For instance, finding users who share the same interests, or visit the same places, can be used to recommend products to them.
- Link prediction: With a graph, you can think of creating intelligent models to predict whether two entities are likely to be connected in the future. Here again, recommendation engines are one possible application of such a tool.
As you can see, networks of all kinds are very well suited to graph databases. But we can go far beyond that view and imagine all kinds of data as a graph, which will open up a lot of new perspectives.
Your data is also a graph
You may have noticed that in the previous image of a social graph, the edges have names. Indeed, some people are friends, while some others have a father/son relationship. Now, let's imagine we can have any kind of relationship, meaning we can start connecting different kinds of entities. For instance, a person is living in a particular country, so (s)he is connected to that country with a relationship of type LIVES_IN. Are you beginning to see the point? With that kind of reasoning, the world itself is a graph and your business is a subpart of it.
Graphs are about relationships, and the world is connected, meaning there are relationships everywhere. We’ll talk about this in more detail in Chapter 3, Empowering Your Business with Pure Cypher, which is dedicated to knowledge graphs.
Graph databases allow you to model the data in that way: nodes, connected by relationships of some type. Let's see how to migrate data stored in relational databases to graph databases.






































































