12.4 Expectation and the variational principle
In section 6.6, we defined the concept of expectation. In section 7.3.4, we further related expectation to observables. Let’s re-express some of those results in terms of eigenvectors uj and eigenvalues λj of a Hermitian matrix A from the last section. expectation observable
Let
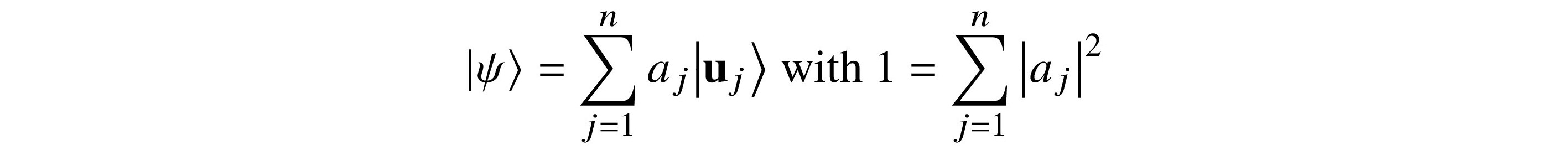
be a quantum state. Each aj = ⟨uj|ψ⟩. Therefore,
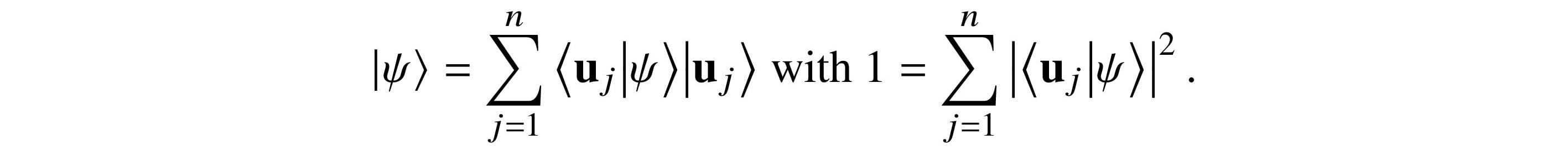
We define
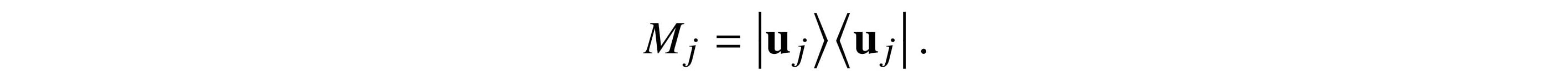
Each Mj is Hermitian and is a projector, meaning that Mj ○ Mj = Mj2 = Mj. We have projector
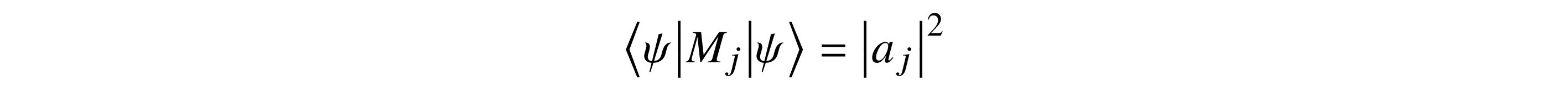
and this is the probability of measuring |uj⟩. The eigenvectors of Mj are the uk for 1 ≤ k ≤ n. The eigenvalue of Mj corresponding to uj is 1. All other eigenvalues are 0.
The Mj are observables since their eigenvectors form a basis for our quantum state vector space by construction.
The expected value, or expectation, ⟨A⟩ of A given the state...























































