The processing from input layer to hidden layer(s) and then to the output layer is called forward propagation. The sum(input*weights)+bias is applied at each layer and then the activation function value is propagated to the next layer. The next layer can be another hidden layer or the output layer. The construction of neural networks uses large number of hidden layers to give rise to Deep Neural Network (DNN).
Once the output is arrived at, at the last layer (the output layer), we compute the error (the predicted output minus the original output). This error is required to correct the weights and biases used in forward propagation. Here is where the derivative function is used. The amount of weight that has to be changed is determined by gradient descent.
The backpropagation process uses the partial derivative of each neuron's activation function to identify the slope (or gradient) in the direction of each of the incoming weights. The gradient suggests how steeply the error will be reduced or increased for a change in the weight. The backpropagation keeps changing the weights until there is greatest reduction in errors by an amount known as the learning rate.
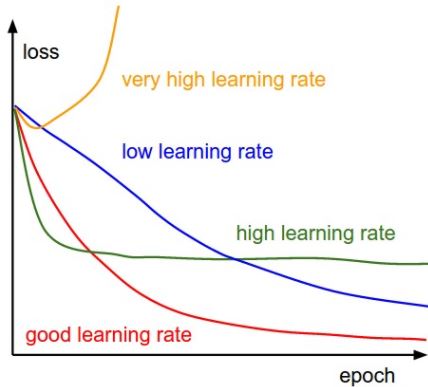
Learning rate is a scalar parameter, analogous to step size in numerical integration, used to set the rate of adjustments to reduce the errors faster. Learning rate is used in backpropagation during adjustment of weights and bias.
More the learning rate, the faster the algorithm will reduce the errors and faster will be the training process: