Understanding scales
Try to learn any melodic instrument and sooner or later you'll learn about scales. If you're trying to compose songs, an understanding of scales is required.
When talking about scales, most music books dive straight into music notation, ask you to memorize scales, and leave you with a book of pages you'll likely never read. I've seen many of these books and lectures and found most of them completely forgettable. We're going to try another approach to help you see why we use scales and how to apply them. This will help you to understand music theory rather than memorize it. In fact, you don't have to memorize much at all; software can do almost all the work for you.
In this chapter, we'll explore answers to the following questions: what are scales, actually? Why do we have them? Why are they important for composing? And how can we apply the music theory of scales in our digital audio workstation?
Let's start by explaining what scales are. All sounds are made up of vibrating molecules in the air. They vibrate in pattern clusters we interpret as wavelengths. Frequency is the term we use to describe the number of wavelengths that pass through the air per second. The following figure shows an example of how we interpret vibrating air molecules as sound waves.
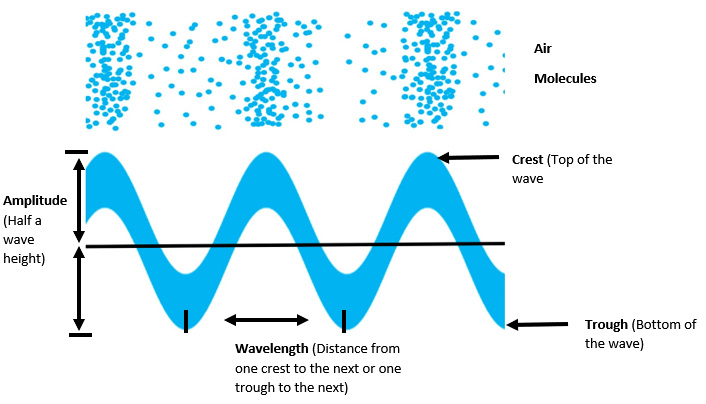
Figure 3.1 – Wavelength
Musical instruments cause air molecules to vibrate at specific frequencies. When air vibrates at a specific constant frequency, our ears interpret the noise as a note pitch. If you have a string instrument, you will be familiar with the idea of tuning your instrument strings to certain frequencies so that when you pluck a string, you get the desired pitch.
We give this a name depending on the audio frequency hit and call it a note pitch. For example, we give the frequency 220 Hz the name A, or more specifically A3, when played on a piano. A chord is defined as three or more notes played together. When you play three or more different audio wavelengths at the same time, you're creating chords.
What happens if we double the frequency of a note? The following figure shows a comparison of a wave form frequency of 220 Hz and 440 Hz.
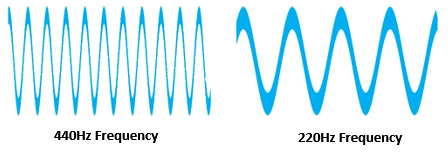
Figure 3.2 – Frequencies
The 440 Hz frequency sounds exactly twice as high as the 220 Hz frequency. We give this interval a name: an octave. An octave is an interval between one musical pitch and another with double the frequency. The two sounds played together sound good. This is true for any two sound frequencies where one is double the frequency of the other. All we've said so far is that a root note pairs nicely with a note an octave apart.
Okay, so the frequency 220 Hz is a note we know as A3 and 440 Hz we know as A4. What about that range between 220 Hz and 440 Hz? Inside that interval, there is a range of frequencies to choose from. If we match the note 220 Hz with a note somewhere in the range of 220Hz and 440Hz, how do we know whether the combination of notes will sound good together?
Over time, we've noticed certain combinations of frequency ratios sound really good together. For example, if we use a note A3 (frequency of 220 Hz) with a note that's an interval ratio of 3:2 (330 Hz), they will sound good together. That second note of 330 Hz is a note commonly known as E3. Trying to think in terms of interval ratios is confusing, though. Instead of trying to remember the names of interval ratios, we use some common terminology. In the case of a 3:2 interval ratio (A3 paired with E3), we use the term perfect fifth.
The following table shows sound intervals that sound pleasant when accompanying a root note. The table is ranked from consonant to dissonant, consonant meaning the sound is in harmony with the root note and dissonant meaning the note doesn't harmonize well with the root note:
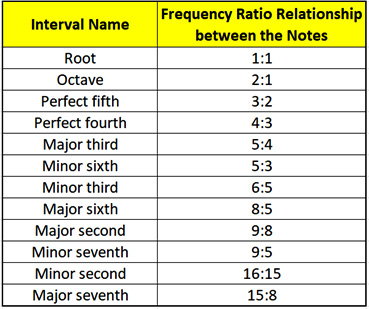
Figure 3.3 – Consonant to dissonant
Take the perfect fifth as an example; the ratio relationship is 3:2. Our ears like the harmony of a root paired up with a sound that has a 3:2 frequency ratio. Our ears like hearing nice, evenly spaced intervals, such as 2:1, 3:2, 4:2, 5:4, and 5:3. As we venture away from these round intervals, our ears interpret the sound as more dissonant.
The most harmonious intervals are the perfect fifth, perfect fourth, major third, and minor third. If you're looking to pair notes with a root note, you'll often want to consider including these intervals.
An octave means you're comparing a root note with a note exactly double its frequency. Western music divides up an octave of music into 12 note intervals. Western music has 12 notes: A, A#, B, C, C#, D, D#, E, F, F#, G, and G#.
The following table organizes notes from smallest frequency to largest frequency assuming that we start with a root note frequency of 220 Hz. It shows the ratio between root notes in relation to other notes:
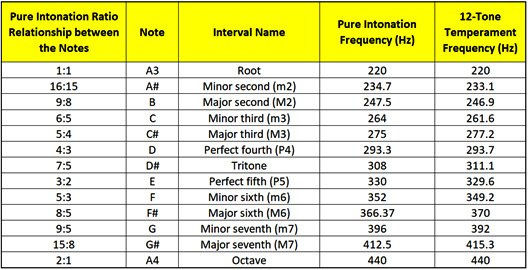
Figure 3.4 – Note intervals
The preceding figure takes the range between 440 Hz and 220 Hz and divides it into 12 interval segments. You can see the note that the frequency is associated with. You may be wondering what the column is about with the title 12-Tone Equal Temperament Frequency (Hz).
What is 12-tone equal temperament frequency (Hz)?
In the 12-Tone Equal Temperament Frequency (Hz) column, you'll notice that some frequencies don't line up perfectly with the ratio. For example, for a root note with a frequency of 220 Hz, a perfect fifth should be 330 Hz. However, in the 12-Tone Equal Temperament Frequency (Hz) column, it says the frequency is 329.6 Hz. In reality, we don't tune our instrument pitch to 330 Hz; we actually tune our instruments to 329.6 Hz. Why would that be?
The reason we tune our instruments differently is so we can easily change keys on our instruments without retuning to a new key. For example, if we were to start with a root note of D# (308 Hz) and pair it with a note that has a frequency ratio of 3:2, that would mean we would need to pair it with an A# note that has a frequency of 462 Hz. But since our instrument is tuned to the key of A, the A# note is 469.3 Hz. This means that our instrument would sound out of tune. So, what do we do to fix this? We tune some notes slightly off intentionally. It's slightly off, but not really noticeably off. Tuning this way gives us the freedom to easily switch the key to our root note and have other notes in the scale sound approximately in tune.
Why does Western music use 12 notes?
Instruments like the violin and trombone allow you to hit notes that are different than 12 notes. You can play frequencies in between the 12 notes. Why are 12 note pitches commonly used? Why not more or less? What about the frequency of 226 Hz or 227 Hz? What about other interval ratios? How come they aren't appearing in this list?
Some musicians in the past have experimented with creating instruments that divide up the octaves into intervals other than 12, such as dividing an octave into 19 or 24 notes. If you play a string or brass instrument, it is possible to hit notes that are other intervals.
Over the years, we realized certain frequencies interval ratios sound good to our ears. Specifically perfect fifth, perfect fourth, major third, and minor third. Using 12 notes ensures we have easy access to the harmonious frequency ratios such as perfect fifths, perfect fourths, major thirds, and minor thirds. Although we could use additional intervals than 12, we find these usually sound more dissonant and are less pleasant to our ears. So, we use 12 notes because it enables us to create sounds that harmonize well.
What are scales?
Scales are select combinations of notes in an octave that complement each other. The notes are ordered from lowest to highest frequency. In Western music, we divide up octaves into 12 note intervals. Scales use fewer notes than 12. They are a selection of notes from the 12 that complement each other. Scales are frameworks that try to force you to play notes that sound good together.
Why are scales important for composing and how do you use scales to compose?
The mood of your music is largely set by the scale you choose. For example, if you only use notes that belong to a minor scale, your music is going to take on a sad or dark tone. If you only use notes that belong to a major scale, your music is going to sound happy and light.
By understanding the mood and tone that belong to each scale, you can choose a scale that matches your desired mood appropriately. In order to do that, we need to know what scales are available to us.
FL Studio offers support for finding what notes are included in a given scale. Let's explore tools to help us compose using scales:
- Load up a melodic instrument such as FL Keys into the Channel rack. If you need a refresher on how to use the Channel rack or Piano roll, we discussed it in Chapter 2, Navigating Through the Key Features of FL Studio.
- Open the Piano roll with your instrument and select the stamp tool.
Figure 3.5 – Stamp tool
A drop-down menu will appear listing a large selection of MIDI note presets. It shows chords, scales, and suggestions for percussive sequences. Of interest to this chapter is the Melodic Scales selection.
- Left-click on a scale such as the Minor Harmonic scale, as shown in the following screenshot:
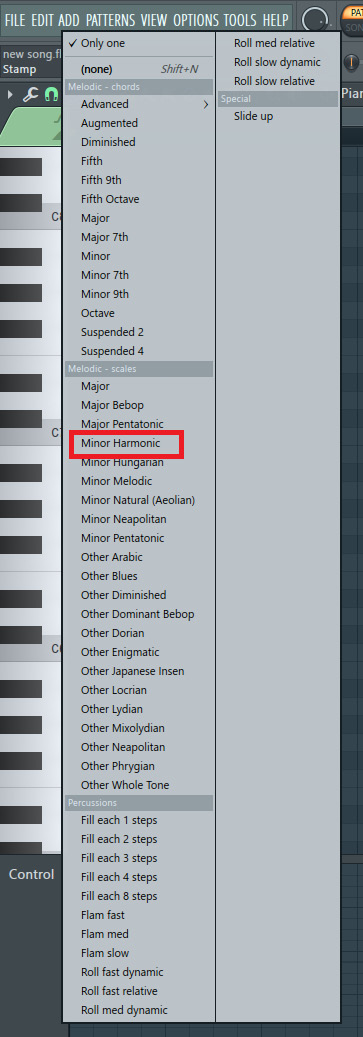
Figure 3.6 – Choose scale
This selects a series of MIDI notes (note pitches) that belong to the minor harmonic scale.
- Left-click anywhere in the grid of the Piano roll to place the notes. After placing the scale notes, you will see something like the following screenshot.
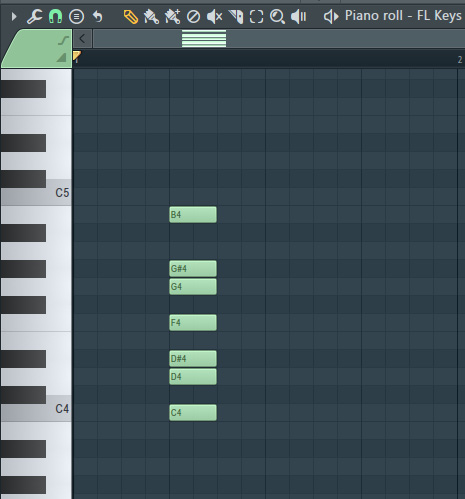
Figure 3.7 – Place notes
The notes you see belong to the minor harmonic scale. In the preceding figure, we happened to start with a tonic note of C. Tonic note means the first note of a scale. The notes that belong to the minor harmonic scale with a tonic note of C are C, D, D#, F, G, G#, and B. As long as I only use these included notes, I will be using notes that fit in the minor harmonic scale. Music in a harmonic minor scale tends to sound sad, beautiful, or dark, so by choosing notes in this scale, I can make my music sound sad, beautiful, or dark.
- Using the Piano roll makes changing keys super easy. Left-click on any of the notes in the Piano roll you added. You'll notice they all get selected as a group. Shift all the notes one pitch higher as shown in the following screenshot:
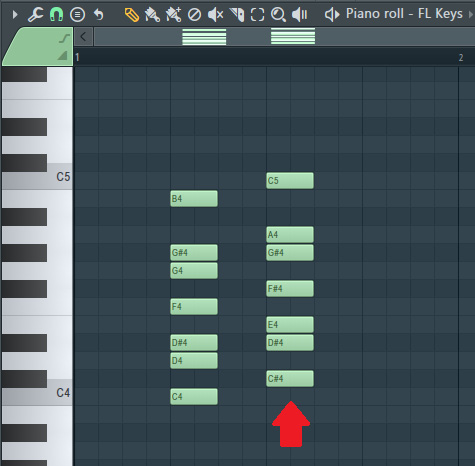
Figure 3.8 – Transpose key
By dragging all the notes up one pitch, we have transposed the notes to a new key. In this case, our notes now have a tonic note of C#. This means we are now using the minor harmonic scale of C# minor instead of C minor. The notes in this C# minor harmonic scale are C#, D#, E, F#, G#, A, and C.
Wow, transposing music to a new key was easy. We didn't have to do any calculations to transpose the notes. All we did was select the notes and move them up or down one an increment and FL Studio did all the work of transposing. If you ever had the task of trying to figure out how to transpose music, you'll realize this is a game changer. Changing musical keys in a Piano roll is incredibly easy, with almost no effort being required in trying to figure out what notes to use.
You have learned what scales are and how to change keys. But you don't yet know how to use them to get the desired tonal moods. For that, we need to introduce the concept of modes.























































