The bias-variance trade-off
In statistical learning, the bias of a model refers to the error of the model introduced by attempting to model a complicated real-life relationship with an approximation. A model with no bias will never make any errors in prediction (like the cookie-area prediction problem). A model with high bias will fail to accurately predict its dependent variable.
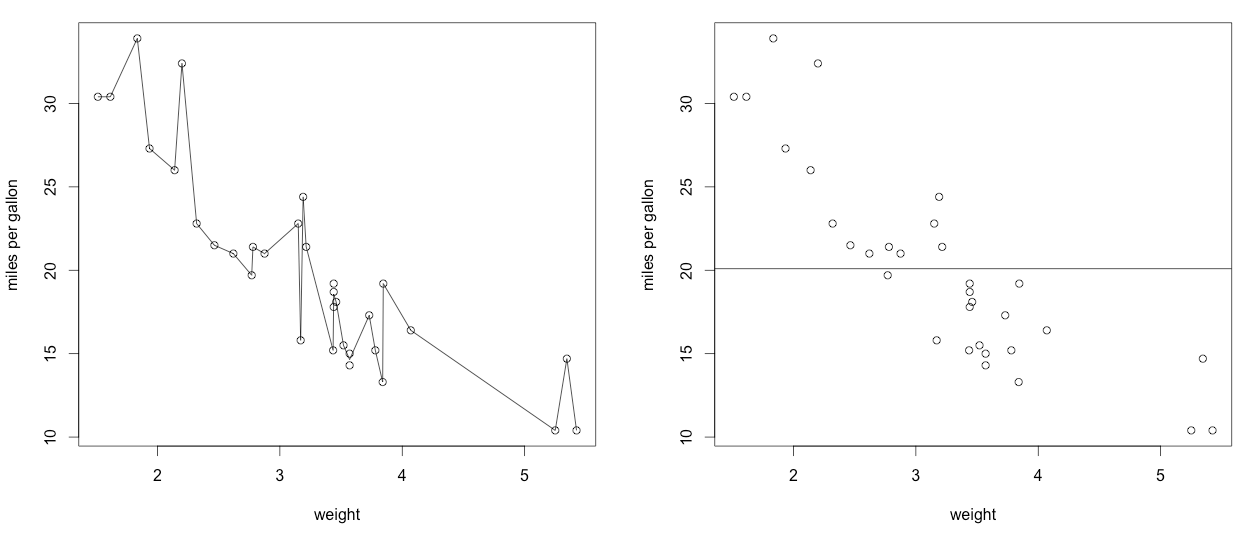
Figure 9.9: The two extremes of the bias-variance trade-off: a complicated model with essentially zero bias (on training data) but enormous variance (left), a simple model with high bias but virtually no variance (right)
The variance of a model refers to how sensitive a model is to changes in the data that built the model. A model with low variance would change very little when built with new data. A linear model with high variance is very sensitive to changes to the data that it was built with, and the estimated coefficients will be unstable.
The term bias-variance trade-off illustrates that it is easy to decrease...











































































