Generating pseudo-random numbers
Generating random numbers is necessary for a large variety of applications, from games to cryptography, from sampling to forecasting. However, the term random numbers is not actually correct, as the generation of numbers through mathematical formulas is deterministic and does not produce true random numbers, but numbers that look random and are called pseudo-random. True randomness can only be achieved through hardware devices, based on physical processes, and even that can be challenged as we may consider even the universe to be actually deterministic. Modern C++ provides support for generating pseudo-random numbers through a pseudo-random number library containing number generators and distributions. Theoretically, it can also produce true random numbers, but in practice, those could actually be only pseudo-random.
Getting ready
In this recipe, we'll discuss the standard support for generating pseudo-random numbers. Understanding the difference between random and pseudo-random numbers is key. True random numbers are numbers that cannot be predicted better than by random chance, and are produced with the help of hardware random number generators. Pseudo-random numbers are numbers produced with the help of algorithms that generate sequences with properties that approximate the ones of true random numbers.
Furthermore, being familiar with various statistical distributions is a plus. It is mandatory, though, that you know what a uniform distribution is, because all engines in the library produce numbers that are uniformly distributed. Without going into any details, we will just mention that uniform distribution is a probability distribution that is concerned with events that are equally likely to occur (within certain bounds).
How to do it...
To generate pseudo-random numbers in your application, you should perform the following steps:
- Include the header
<random>:#include <random> - Use an
std::random_devicegenerator for seeding a pseudo-random engine:std::random_device rd{}; - Use one of the available engines for generating numbers and initialize it with a random seed:
auto mtgen = std::mt19937{ rd() }; - Use one of the available distributions for converting the output of the engine to one of the desired statistical distributions:
auto ud = std::uniform_int_distribution<>{ 1, 6 }; - Generate the pseudo-random numbers:
for(auto i = 0; i < 20; ++i) auto number = ud(mtgen);
How it works...
The pseudo-random number library contains two types of components:
- Engines, which are generators of random numbers; these can produce either pseudo-random numbers with a uniform distribution or, if available, actual random numbers.
- Distributions that convert the output of an engine to a statistical distribution.
All engines (except for random_device) produce integer numbers in a uniform distribution, and all engines implement the following methods:
min(): This is a static method that returns the minimum value that can be produced by the generator.max(): This is a static method that returns the maximum value that can be produced by the generator.seed(): This initializes the algorithm with a start value (except forrandom_device, which cannot be seeded).operator(): This generates a new number uniformly distributed betweenmin()andmax().discard(): This generates and discards a given number of pseudo-random numbers.
The following engines are available:
linear_congruential_engine: This is a linear congruential generator that produces numbers using the following formula:x(i) = (A * x(i – 1) + C) mod M
mersenne_twister_engine: This is a Mersenne twister generator that keeps a value on W * (N – 1) * R bits. Each time a number needs to be generated, it extracts W bits. When all the bits have been used, it twists the large value by shifting and mixing the bits so that it has a new set of bits to extract from.subtract_with_carry_engine: This is a generator that implements a subtract with carry algorithm based on the following formula:x(i) = (x(i – R) – x(i – S) – cy(i – 1)) mod M
In the preceding formula, cy is defined as:

In addition, the library provides engine adapters that are also engines wrapping another engine and producing numbers based on the output of the base engine. Engine adapters implement the same methods mentioned earlier for the base engines. The following engine adapters are available:
discard_block_engine: A generator that, from every block of P numbers generated by the base engine, keeps only R numbers, discarding the rest.independent_bits_engine: A generator that produces numbers with a different number of bits than the base engine.shuffle_order_engine: A generator that keeps a shuffled table of K numbers produced by the base engine and returns numbers from this table, replacing them with numbers generated by the base engine.
Choosing a pseudo-random number generator should be done based on the specific requirements of your application. The linear congruential engine is medium fast but has very small storage requirements for its internal state. The subtract with carry engine is very fast, including on machines that don't have a processor with advanced arithmetic instructions set. However, it requires larger storage for its internal state and the sequence of generated numbers has fewer desirable characteristics. The Mersenne twister is the slowest of these engines and has the greatest storage durations, but produces the longest non-repeating sequences of pseudo-numbers.
All these engines and engine adaptors produce pseudo-random numbers. The library, however, provides another engine called random_device that is supposed to produce non-deterministic numbers, but this is not an actual constraint as physical sources of random entropy might not be available. Therefore, implementations of random_device could actually be based on a pseudo-random engine. The random_device class cannot be seeded like the other engines and has an additional method called entropy() that returns the random device entropy, which is 0 for a deterministic generator and nonzero for a non-deterministic generator.
However, this is not a reliable method for determining whether the device is actually deterministic or non-deterministic. For instance, both GNU libstdc++ and LLVM libc++ implement a non-deterministic device, but return 0 for entropy. On the other hand, VC++ and boost.random return 32 and 10, respectively, for entropy.
All these generators produce integers in a uniform distribution. This is, however, only one of the many possible statistical distributions where random numbers are needed in most applications. To be able to produce numbers (either integer or real) in other distributions, the library provides several classes called distributions. These convert the output of an engine according to the statistical distribution it implements. The following distributions are available:
|
Type |
Class name |
Numbers |
Statistical distribution |
|
Uniform |
|
Integer |
Uniform |
|
|
Real |
Uniform |
|
|
Bernoulli |
|
Boolean |
Bernoulli |
|
|
Integer |
Binomial |
|
|
|
Integer |
Negative binomial |
|
|
|
Integer |
Geometric |
|
|
Poisson |
|
Integer |
Poisson |
|
|
Real |
Exponential |
|
|
|
Real |
Gamma |
|
|
|
Real |
Weibull |
|
|
|
Real |
Extreme value |
|
|
Normal |
|
Real |
Standard normal (Gaussian) |
|
|
Real |
Lognormal |
|
|
|
Real |
Chi-squared |
|
|
|
Real |
Cauchy |
|
|
|
Real |
Fisher's F-distribution |
|
|
|
Real |
Student's t-distribution |
|
|
Sampling |
|
Integer |
Discrete |
|
|
Real |
Values distributed on constant subintervals |
|
|
|
Real |
Values distributed on defined subintervals |
Each of the engines provided by the library has advantages and disadvantages, as it was mentioned earlier. The Mersenne twister, although the slowest and one that has the largest internal state, when initialized appropriately, can produce the longest non-repeating sequence of numbers. In the following examples, we will use std::mt19937, a 32-bit Mersenne twister with 19,937 bits of internal state.
The simplest way to generate random numbers looks like this:
auto mtgen = std::mt19937 {};
for (auto i = 0; i < 10; ++i)
std::cout << mtgen() << '\n';
In this example, mtgen is std::mt19937 for the Mersenne twister. To generate numbers, you only need to use the call operator that advances the internal state and returns the next pseudo-random number. However, this code is flawed, as the engine is not seeded. As a result, it always produces the same sequence of numbers, which is probably not what you want in most cases.
There are different approaches for initializing the engine. One approach, common with the C random library, is to use the current time. In modern C++, it should look like this:
auto seed = std::chrono::high_resolution_clock::now()
.time_since_epoch()
.count();
auto mtgen = std::mt19937{ static_cast<unsigned int>(seed) };
In this example, seed is a number representing the number of ticks since the clock's epoch until the present moment. This number is then used to seed the engine. The problem with this approach is that the value of that seed is actually deterministic, and in some classes of applications, it could be prone to attacks. A more reliable approach is to seed the generator with actual random numbers.
The std::random_device class is an engine that is supposed to return true random numbers, though implementations could actually be based on a pseudo-random generator:
std::random_device rd;
auto mtgen = std::mt19937 {rd()};
Numbers produced by all engines follow a uniform distribution. To convert the result to another statistical distribution, we have to use a distribution class. To show how generated numbers are distributed according to the selected distribution, we will use the following function. This function generates a specified number of pseudo-random numbers and counts their repetition in a map. The values from the map are then used to produce a bar-like diagram showing how often each number occurred:
void generate_and_print(std::function<int(void)> gen,
int const iterations = 10000)
{
// map to store the numbers and their repetition
auto data = std::map<int, int>{};
// generate random numbers
for (auto n = 0; n < iterations; ++n)
++data[gen()];
// find the element with the most repetitions
auto max = std::max_element(
std::begin(data), std::end(data),
[](auto kvp1, auto kvp2) {
return kvp1.second < kvp2.second; });
// print the bars
for (auto i = max->second / 200; i > 0; --i)
{
for (auto kvp : data)
{
std::cout
<< std::fixed << std::setprecision(1) << std::setw(3)
<< (kvp.second / 200 >= i ? (char)219 : ' ');
}
std::cout << '\n';
}
// print the numbers
for (auto kvp : data)
{
std::cout
<< std::fixed << std::setprecision(1) << std::setw(3)
<< kvp.first;
}
std::cout << '\n';
}
The following code generates random numbers using the std::mt19937 engine with a uniform distribution in the range [1, 6]; this is basically what you get when you throw a dice:
std::random_device rd{};
auto mtgen = std::mt19937{ rd() };
auto ud = std::uniform_int_distribution<>{ 1, 6 };
generate_and_print([&mtgen, &ud]() {return ud(mtgen); });
The output of the program looks like this:

Figure 2.1: Uniform distribution of the range [1,6]
In the next and final example, we're changing the distribution to a normal distribution with a mean of 5 and a standard deviation of 2. This distribution produces real numbers; therefore, in order to use the previous generate_and_print() function, the numbers must be rounded to integers:
std::random_device rd{};
auto mtgen = std::mt19937{ rd() };
auto nd = std::normal_distribution<>{ 5, 2 };
generate_and_print(
[&mtgen, &nd]() {
return static_cast<int>(std::round(nd(mtgen))); });
The following will be the output of the preceding code:
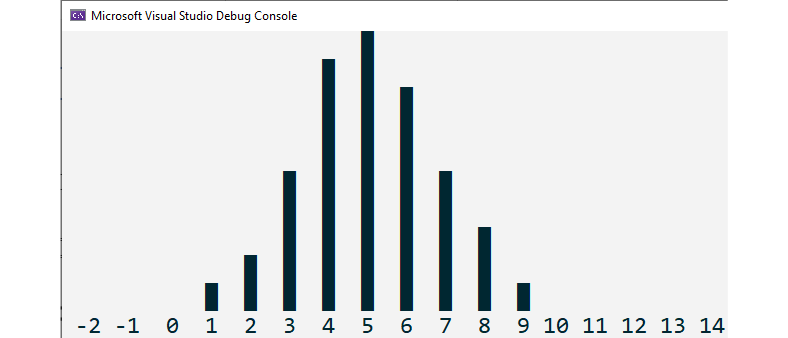
Figure 2.2: Normal distribution with mean 5 and standard variance 2
Here, we can see that, based on the graphical representation, the distribution has changed from a uniform one to a normal one with the mean at value 5.
See also
- Initializing all bits of internal state of a pseudo-random number generator to learn how to properly initialize random number engines




























































