Fibonacci sequence - a simple recursion and two performance improvements

The Fibonacci sequence is a sequence of numbers where each number is equal to the previous two numbers added together. Here's an example of this:

 1  1  2  3  5  8  13  21  34

So, 1 plus 1 is 2, 2 plus 3 is 5, 5 plus 8 is 13, and so on.

Let's use the Fibonacci sequence to help illustrate a number of concepts.

A recursive function is a function that calls itself in order to break down complex input into simpler ones. With each recursive call, the input problem must be simplified in such a way that eventually the base case must be reached.

The Fibonacci sequence can be easily implemented as a recursive function:

func Fibonacci(x int) int {
    if x == 0 {
        return 0
    } else if x <= 2 {
        return 1
    } else {
        return Fibonacci(x-2) + Fibonacci(x-1)
    }
}

In the preceding recursive function (Fibonacci), if the input is the simple case of 0 then it returns 0. Similarly, if the input is 1 or 2 then return 1.

An input of 0, 1 or 2 is called the base case or stopping condition; else, fib will call itself twice, adding the previous value in the sequence to the one preceding it:

Fibonacci(5) calculation graph

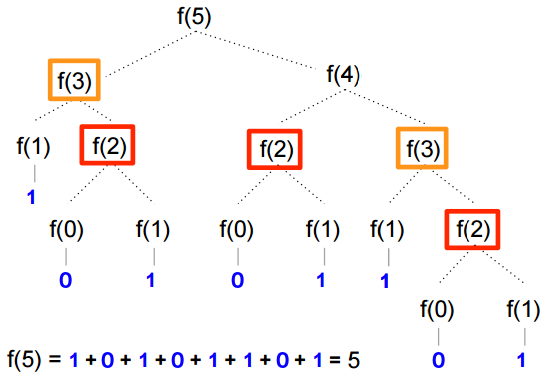
In the preceding figure Fibonacci(5) calculation graph, we can visually see how the fifth element in the Fibonacci sequence is calculated. We see f(3) is calculated twice and f(2) is calculated thrice. Only the final leaf nodes of 1 are added together to calculate the sum total of 5:

func main() {
   fib := Fibonacci
   fmt.Printf("%vn", fib(5))
}

Run that code and you'll get 5. Recursive functions perform identical calculations over and over again; f(3) is calculated twice and f(2) is calculated thrice. The deeper the graph, the more redundant calculations get executed. That is terribly inefficient. Try it yourself. Pass a value greater than 50 to fib and see how long you have to wait for the final result.

Go provides many ways to improve this performance. We'll look at two options: memoization and concurrency.

Memoization is an optimization technique used to increase performance by storing the results of expensive function calls and returning the cached result when the same input occurs again.

Memoization works well because of the following two properties of pure functions:

• They always return the same result given the same input(s)
• They have no side effects in the environment in which they run

Memoization

Let's utilize a memoization technique to speed up our Fibonacci calculation.

First, let's create a function type named Memoized() and define our Fibonacci variable to be of that type:

type Memoized func(int) int
var fibMem Memoized

Next, let's implement the Memoize() function. The key thing to realize here is that as soon as our application starts, even before our main() function is executed, our fibMem variable get wired up. If we were to step through our code we'd see that our Memoize function is called. The cache variable is assigned and our anonymous function is returned and assigned to our fibMem function literal variable.

func Memoize(mf Memoized) Memoized {
       cache := make(map[int]int)
       return func(key int) int {
              if val, found := cache[key]; found {
                     return val
              }
              temp := mf(key)
              cache[key] = temp
              return temp
       }
}

Memoize takes a Memoized() function type as its input and returns a Memoized() function.

In the first line of Memoize, we create a variable of the type map to act as our cache in order to hold computed Fibonacci computations.

Next, we create a closure that is of the type Memoized(), which is returned by the Memoize() function. Note that a closure is an inner function that closes over or that has access to variables in its outer scope.

Inside the closure, if we find the computation for the passed integer, we return its value from the cache; else we call the recursive Fibonacci function (mf) with the integer parameter (key), whose return value will be stored in cache[key]. Next time, when the same key is requested its value will be returned directly from the cache.

An anonymous function is a function defined with no name. When an anonymous function includes logic that can access variables defined in its scope, for example, cache, and if that anonymous function can be passed as an argument or returned as the value of function calls, which is true in this case, then we can refer to this anonymous function as a lambda expression.

We'll implement the logic of the Fibonacci Sequence in a function named fib:

func fib(x int) int {
   if x == 0 {
      return 0
   } else if x <= 2 {
      return 1
   } else {
      return fib(x-2) + fib(x-1)
   }
}

The last thing we do in our memoize.go file is to create the following function:

func FibMemoized(n int) int {
   return fibMem(n)
}

Now, it's time to see if our wiring works properly. In our main() function when we execute our println statement, we get the correct output.

println(fibonacci.FibMemoized(5))

The following is the output:

5

We can verify that 5 is the correct answer by glancing back at our Fibonacci(5) calculation graph shown earlier in this chapter.

If we were to step through our code using a debugger, we'd see that fibonacci.FibMemoized(5) calls the following

func FibMemoized(n int) int {
   return fibMem(n)
}

And the value of n variable is 5. Since fibMem is pre-wired, we start executing at the return statement (and we have access to the cache variable that has already been initialized) . So, we begin executing at the return statement shown in the following code (from the Memoize function):

return func(key int) int {
   if val, found := cache[key]; found {
      return val
   }
   temp := mf(key)
   cache[key] = temp
   return temp
}

Since this is the first time through, there are no entries in the cache and we skip past the body of the if block and run temp := mf(key)

That calls the fib function:

func fib(x int) int {
   if x == 0 {
      return 0
   } else if x <= 2 {
      return 1
   } else {
      return fib(x-2) + fib(x-1)
   }
}

Run the fib function as follows:

Since x is greater than 2 we run the last else statement that recursively calls fib twice. Recursive calls to fib continues until the base conditions are reached and the final result is calculated and returned.