Theoretical overview
Let the random variable X represent the random loss that we would like to model, with F(x) = P(X ≤ x) as its distribution function. For a given threshold u, the excess loss over the threshold Y = X – u has the following distribution function:
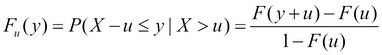
For a large class of underlying loss distributions, the Fu(y) distribution of excess losses over a high threshold u converges to a Generalized Pareto distribution (GPD) as the threshold rises toward the right endpoint of the loss distribution. This follows from an important limit theorem in EVT. For details, the reader is referred to McNeil, Frey, and Embrechts (2005). The cumulative distribution function of GPD is the following:
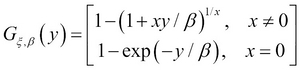
Here ξ is generally referred to as the shape parameter and β as the scale parameter.
Though strictly speaking, the GPD is only the limiting distribution for excess losses over a high threshold, however, it serves as the natural model of the excess loss distribution even for finite thresholds. In other words...






















































