As seen in other algorithms, in order to perform aggregations, we need to define a distance metric first, which represents the dissimilarity between samples. We have already analyzed many of them but, in this context, it's helpful to start considering the generic Minkowski distance (parametrized with p):
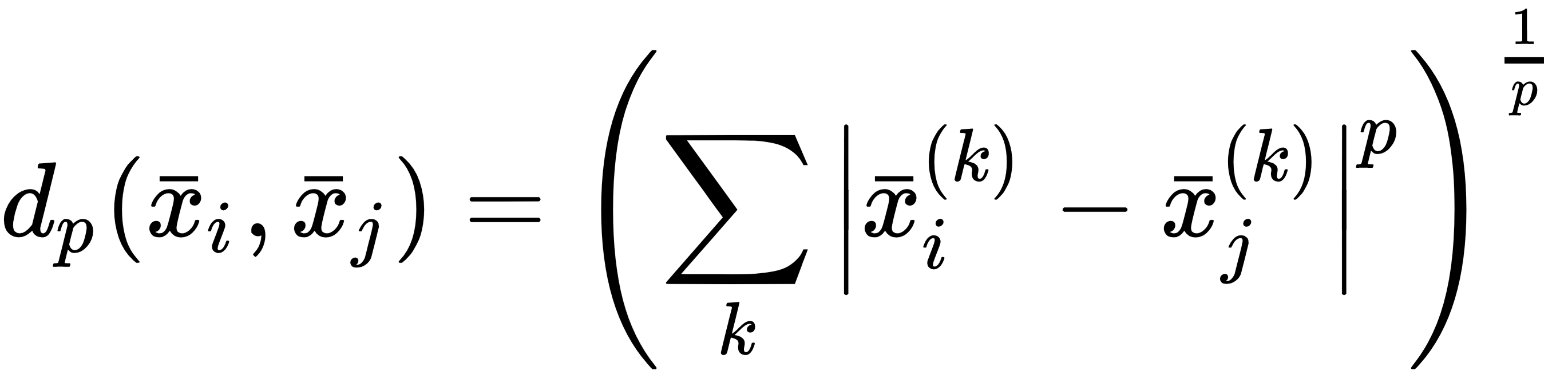
Two particular cases correspond to p=2 and p=1. In the former case, when p=2, we obtain the standard Euclidean distance (equivalent to the L2 norm):
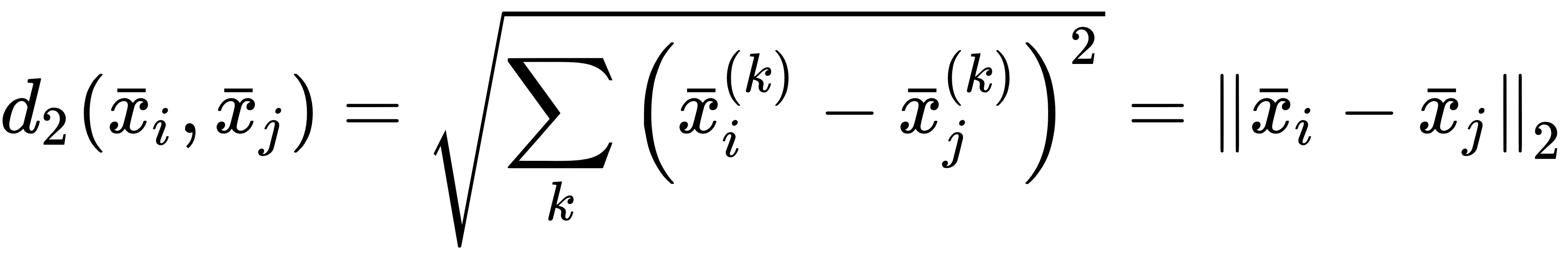
When p=1, we obtain the Manhattan or city block distance (equivalent to the L1 norm):
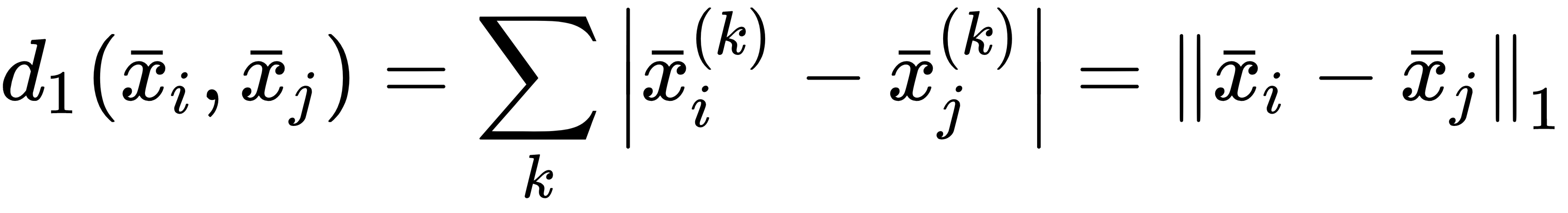
The main differences between these distances were discussed in Chapter 2, Clustering Fundamentals. In this chapter, it's useful to introduce the cosine distance, which is not a proper distance metric (from a mathematical point of view), but it is very helpful when the discrimination between samples must depend...
























































