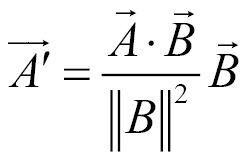Projection
Sometimes it's useful to decompose a vector into parallel and perpendicular components with respect to another vector. Projecting  onto
onto  will give us the length of
will give us the length of  in the direction of
in the direction of  . This projection decomposes
. This projection decomposes  into its parallel component with respect to
into its parallel component with respect to  . Once we know the parallel component of
. Once we know the parallel component of  , we can use it to get the perpendicular component. The formula for projecting
, we can use it to get the perpendicular component. The formula for projecting  onto
onto  is as follows:
is as follows:
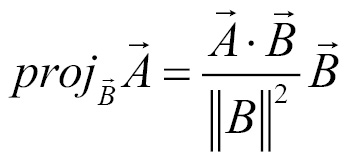
The perpendicular component of  with respect to
with respect to  is defined as follows:
is defined as follows:
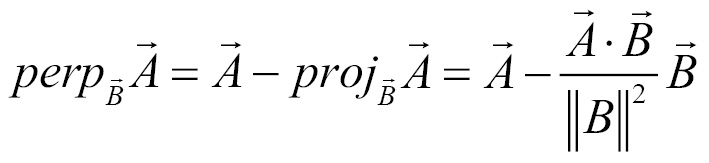
Getting ready
Implementing the projection is fairly straightforward as we already have both the dot product and magnitude squared defined. In the following function, the vector being projected is represented by the variable length, and the vector it is being projected onto is represented by the variable direction. If we compare it to the preceding formula, length is  , and
, and direction is  .
.
How to do it…
Follow these steps to implement projection functions for two and three dimensional vectors. A function to get the perpendicular component of the projection is also described:
- Declare the projection and perpendicular functions in
vectors.h:vec2 Project(const vec2& length, const vec2& direction); vec3 Project(const vec3& length, const vec3& direction); vec2 Perpendicular(const vec2& len, const vec2& dir); vec3 Perpendicular(const vec3& len, const vec3& dir);
- Add the implementation of projection to
vectors.cpp:vec2 Project(const vec2& length, const vec2& direction) { float dot = Dot(length, direction); float magSq = MagnitudeSq(direction); return direction * (dot / magSq); } vec3 Project(const vec3& length, const vec3& direction) { float dot = Dot(length, direction); float magSq = MagnitudeSq(direction); return direction * (dot / magSq); } - Add the implementation of perpendicular to
vectors.cpp:vec2 Perpendicular(const vec2& len, const vec2& dir) { return len - Project(len, dir); } vec3 Perpendicular(const vec3& len, const vec3& dir) { return len - Project(len, dir); }
How it works…
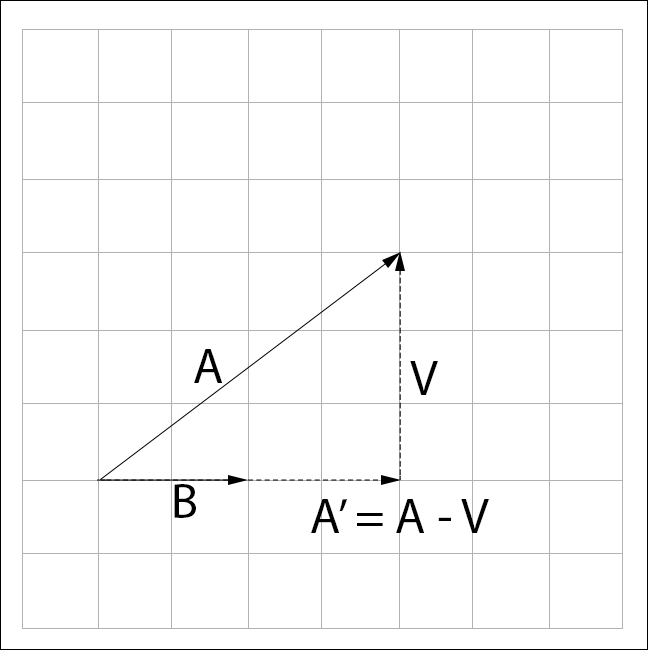
Let's explore how projection works. Say we want to project  onto
onto  , to find
, to find  . Having a ' character next to a vector means prime; it's a transformed version of the vector;
. Having a ' character next to a vector means prime; it's a transformed version of the vector;  is pronounced A-Prime:
is pronounced A-Prime:
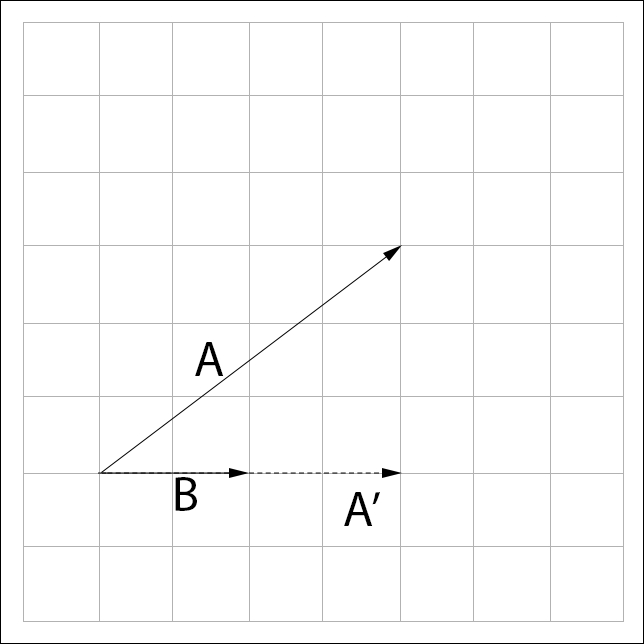
From the preceding figure we see that  can be found by subtracting some unknown vector from
can be found by subtracting some unknown vector from  . This unknown vector is the perpendicular component of
. This unknown vector is the perpendicular component of  with respect to
with respect to  , let's call it
, let's call it  :
:
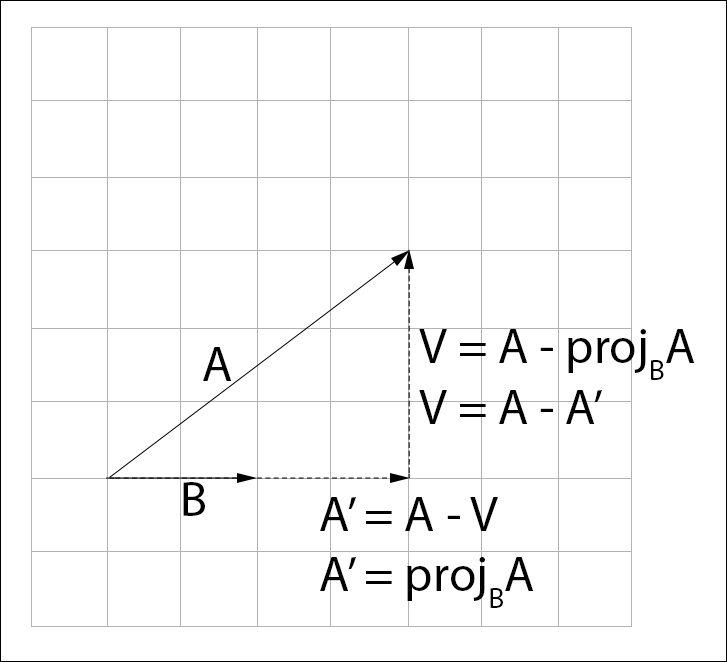
We can get the perpendicular component  by subtracting the projection of
by subtracting the projection of  onto
onto  from
from . The projection at this point is still unknown, that's what we are trying to find:
. The projection at this point is still unknown, that's what we are trying to find:
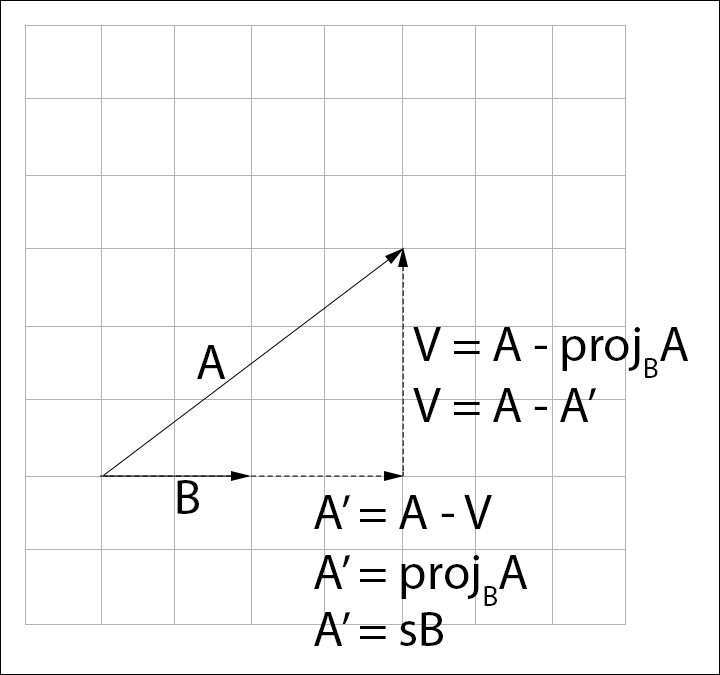
Because  points in the same direction as
points in the same direction as  , we can express
, we can express  as scaling
as scaling  by some unknown scalar s,
by some unknown scalar s,  . Knowing this, the problem becomes, how do we find s?:
. Knowing this, the problem becomes, how do we find s?:
The dot product of two perpendicular vectors is 0. Because of this, the dot product of  and
and  is going to be 0:
is going to be 0:
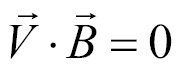
Substitute the value of  with the equation we use to find its value,
with the equation we use to find its value,  :
:
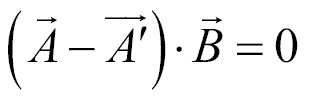
Finally, let's substitute  with the equation we use to find its value,
with the equation we use to find its value,  :
:
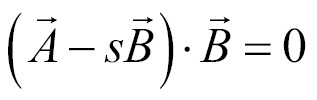
Now the only unknown in the formula is s, let's try to find it. The dot product exhibits the distributive property, let's distribute  :
:
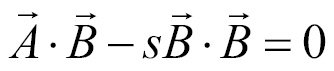
Let's start to isolate s, first we add  to both sides of the equation:
to both sides of the equation:
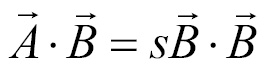
Now we can isolate s if we divide both sides of the equation by  . Remember, the dot product of a vector with itself yields the square magnitude of that vector:
. Remember, the dot product of a vector with itself yields the square magnitude of that vector:
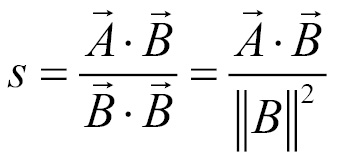
Now we can solve  by substituting s with the preceding formula. The final equation becomes:
by substituting s with the preceding formula. The final equation becomes: