A sense of balance
Many data structures have a balance invariant. After every update to the tree, the invariant is restored by rebalancing the structure. Why do we need this balancing? What do we mean by balance?
A Binary Search Tree, for example, could degenerate into a list. For example, consider a scenario where you insert sorted data into a BST. You will get a tree whose nodes have no left children. To all intents and purposes, you have constructed just a linked list in the garb of a tree. This would lead to pathetic access performance for O(n). A balanced BST won't have this problem.
A tree is perfectly balanced if the left and right subtrees of any node are of the same height.
We also have almost perfectly balanced trees. The subtrees' heights may differ by at most 1.
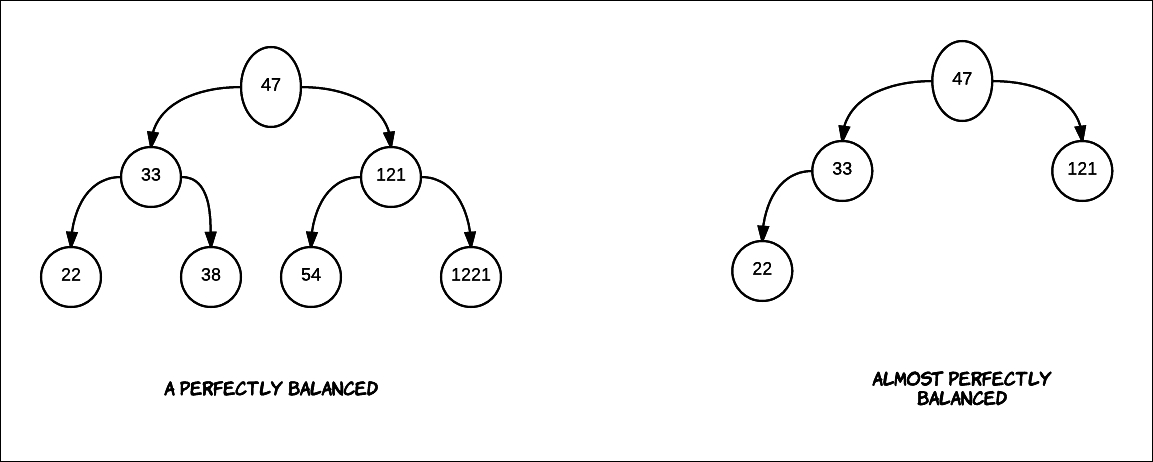
As we will soon see in the next chapter, balancing a BST allows us to have guaranteed O(logn) search times. The next chapter discusses Red-Black trees, which are a very popular balanced variant of the...


































































