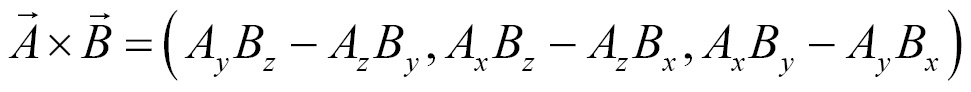Cross product
The cross product is written as a X between two vectors,  . It returns a new vector that is perpendicular to both vectors
. It returns a new vector that is perpendicular to both vectors  and
and  . That is, the result of the cross product points 90 degrees from both vectors.
. That is, the result of the cross product points 90 degrees from both vectors.
The cross product is defined only for three-dimensional vectors. This is because any two non-parallel vectors form a plane, and there will always exist a line perpendicular to that plane. As such, we will only be implementing the cross product for the vec3 structure.
The equation of the cross product is as follows:
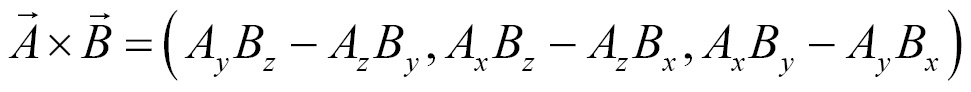
Getting ready
The formula behind the cross product seems large and complicated. We're going to implement a pattern in code that hopefully will make remembering this formula easy.
How to do it…
The cross product is only well defined for three dimensional vectors. Follow these steps to implement the cross product in an intuitive way:
- Add the declaration for the cross product to
vectors.h:vec3 Cross(const vec3& l, const vec3& r);
- Start the implementation in
vectors.cpp:vec3 Cross(const vec3& l, const vec3& r) { vec3 result; // We will add more code here return resut; } - Start by listing out the
x,y, andzcomponents of the result in a column:vec3 Cross(const vec3& l, const vec3& r) { vec3 result; result.x = /* Will finish in step 6 */ result.y = /* Will finish in step 6 */ result.z = /* Will finish in step 6 */ return resut; } - Flesh out the first row by multiplying
l.yandr.z. Notice how the first column containsx,y, andzcomponents in order and so does the first row:vec3 Cross(const vec3& l, const vec3& r) { vec3 result; result.x = l.y * r.z /* Will finish in step 6 */ result.y = /* Will finish in step 6 */ result.z = /* Will finish in step 6 */ return resut; } - Follow the
x,y,zpattern for the rest of the rows. Start each row with the appropriate letter following the letter of the first column:vec3 Cross(const vec3& l, const vec3& r) { vec3 result; result.x = l.y * r.z /* Will finish in step 6 */ result.y = l.z * r.x /* Will finish in step 6 */ result.z = l.x * r.y /* Will finish in step 6 */ return resut; } - Finally, complete the function by subtracting the mirror components of the multiplication from each row:
vec3 Cross(const vec3& l, const vec3& r) { vec3 result; result.x = l.y * r.z - l.z * r.y; result.y = l.z * r.x - l.x * r.z; result.z = l.x * r.y - l.y * r.x; return resut; // Done }
How it works…
We're going to explore the cross product using three normal vectors that we know to be perpendicular. Let vector  ,
,  , and
, and  represents the basis of
represents the basis of  , three-dimensional space. This means we define the vectors as follows:
, three-dimensional space. This means we define the vectors as follows:
 points right; it is of unit length on the x axis:
points right; it is of unit length on the x axis: 
 points up; it is of unit length on the y axis:
points up; it is of unit length on the y axis: 
 points forward; it is of unit length on the z axis:
points forward; it is of unit length on the z axis: 
Each of these vectors are orthogonal to each other, meaning they are 90 degrees apart. This makes all of the following statements about the cross product true:
-
Right X Up = Forward,

-
Up X Forward = Right,

-
Forward X Right = Up,

The cross product is not cumulative,  is not the same as
is not the same as  . Let's see what happens if we flip the operands of the preceding formulas:
. Let's see what happens if we flip the operands of the preceding formulas:
-
Up X Right = Backward,

-
Forward X Up = Left,

-
Right X Forward = Down,

Matrices will be covered in the next chapter, if this section is confusing, I suggest re-reading it after the next chapter. One way to evaluate the cross product is to construct a 3x3 matrix. The top row of the matrix consists of vector  ,
,  , and
, and  . The next row comprises the components of the vector on the left side of the cross product, and the final row comprises the components of the vector on the right side of the cross product. We can then find the cross product by evaluating the pseudo-determinant of the matrix:
. The next row comprises the components of the vector on the left side of the cross product, and the final row comprises the components of the vector on the right side of the cross product. We can then find the cross product by evaluating the pseudo-determinant of the matrix:
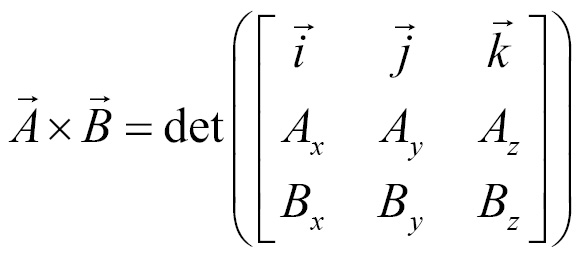
We will discuss matrices and determinants in detail in Chapter 2, Matrices. For now, the preceding determinant evaluates to the following:
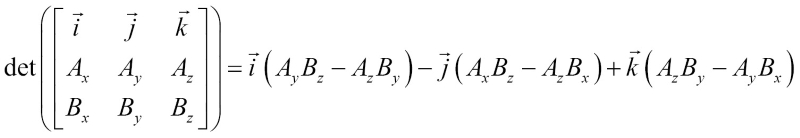
The result of  is a scalar, which is then multiplied by the
is a scalar, which is then multiplied by the  vector. Because the
vector. Because the  vector was a unit vector on the x axis, whatever the scalar is will be in the x axis of the resulting vector. Similarly, whatever
vector was a unit vector on the x axis, whatever the scalar is will be in the x axis of the resulting vector. Similarly, whatever  is multiplied by will only have a value on the y axis and whatever
is multiplied by will only have a value on the y axis and whatever  is multiplied by will only have a value on the z axis. The preceding determinant simplifies to the following:
is multiplied by will only have a value on the z axis. The preceding determinant simplifies to the following: