Performing iterative updates using the Velocity Verlet algorithm
As particles move in a system over time, the separation  between each pair of particles changes accordingly, resulting in a change of the derivatives described in the previous section—that is, the force becomes time-dependent. Therefore, the trajectory is updated over a small increment of time called the timestep
between each pair of particles changes accordingly, resulting in a change of the derivatives described in the previous section—that is, the force becomes time-dependent. Therefore, the trajectory is updated over a small increment of time called the timestep  , and by iteratively updating the trajectory over a large number of timesteps, a complete trajectory can be obtained.
, and by iteratively updating the trajectory over a large number of timesteps, a complete trajectory can be obtained.
The purpose of keeping the timestep small is to ensure that the particles do not undergo drastic changes in position and therefore conserve energy in the system. For atomic masses, especially in the presence of forces from molecular bonds, angles, and dihedrals, a timestep of approximately 1 femtosecond is typically employed.
An advantage of using a small timestep is that the net force  acting on a particle can be approximated to remain constant in the duration of the timestep. Therefore, the equations of motion that iteratively update the trajectory at timestep increments become the following:
acting on a particle can be approximated to remain constant in the duration of the timestep. Therefore, the equations of motion that iteratively update the trajectory at timestep increments become the following:
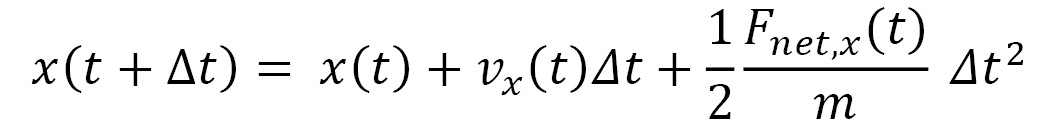
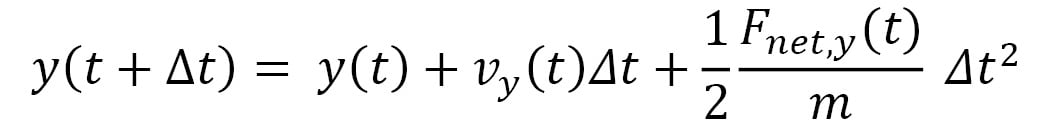
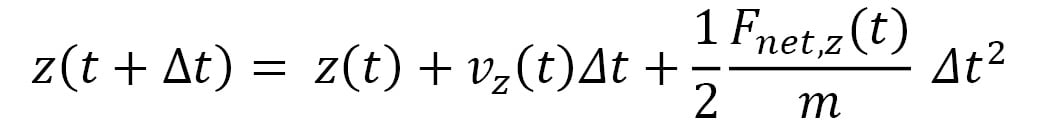
Here,  represents the velocity vector of the particle, and its components are iteratively updated by the following:
represents the velocity vector of the particle, and its components are iteratively updated by the following:
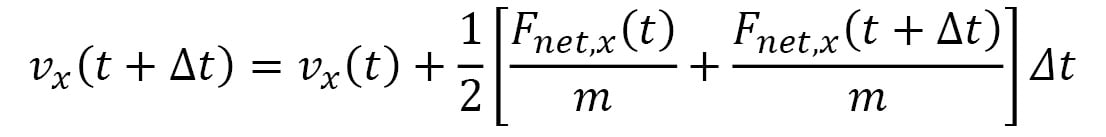
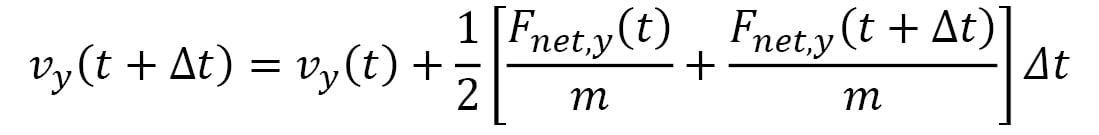
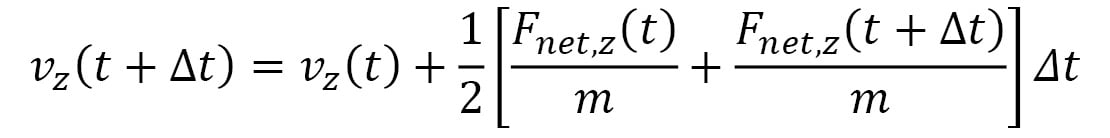
Here, the terms within the [ ] represent the average acceleration in each dimension, calculated using the accelerations at time t and the following iteration,  . This is known as the Velocity Verlet algorithm, which considerably reduces errors over a long simulation period as compared to algorithms that use the acceleration at a single point in time (for example, the Euler algorithm). Furthermore, the Velocity Verlet algorithm is able to conserve energy and momentum within rounding errors with a sufficiently small timestep, unlike the Euler algorithm, which can lead to an indefinite increase in energy over time.
. This is known as the Velocity Verlet algorithm, which considerably reduces errors over a long simulation period as compared to algorithms that use the acceleration at a single point in time (for example, the Euler algorithm). Furthermore, the Velocity Verlet algorithm is able to conserve energy and momentum within rounding errors with a sufficiently small timestep, unlike the Euler algorithm, which can lead to an indefinite increase in energy over time.
In effect, the position and velocity of each particle are tabulated at each iteration, as illustrated in the following table:

Table 1.1 – Table showing sequence of iterative update of position and velocity vectors of each particle
This table shows the sequence of iterative update of point particles that undergo a linear motion without any rotational component. In the case of a non-point object such as a rigid body, both linear and rotational motion must be incorporated for a proper treatment of its dynamics. Similar to linear motion, rotational motion of rigid bodies can be iteratively updated using a similar algorithm, as discussed next.
































































