12.4 Expectation and the variational principle

In section 6.6, we defined the concept of expectation. In section 7.3.4, we further related expectation to observables. Let’s re-express some of those results in terms of eigenvectors u_j and eigenvalues λ_j of a Hermitian matrix A from the last section. expectation observable

Let

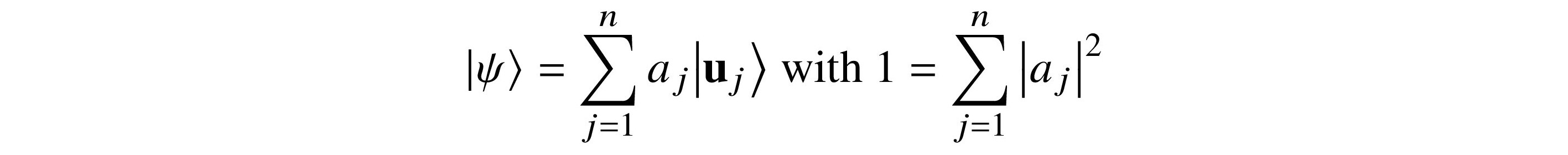
be a quantum state. Each a_j = ⟨u_j|ψ⟩. Therefore,

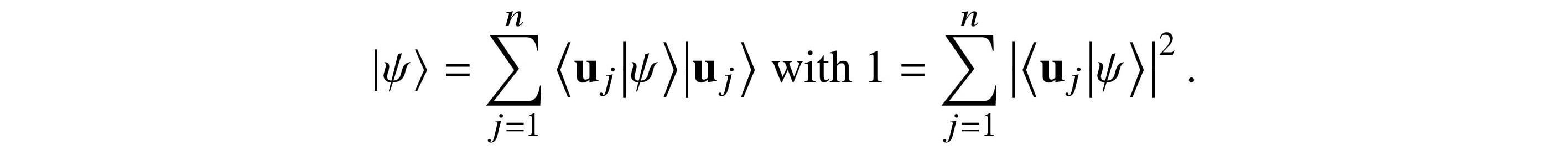
We define

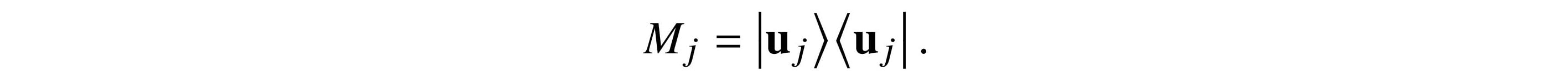
Each M_j is Hermitian and is a projector, meaning that M_j ○ M_j = M_j² = M_j. We have projector

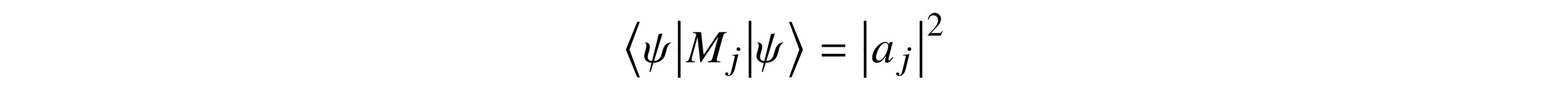
and this is the probability of measuring |u_j⟩. The eigenvectors of M_j are the u_k for 1 ≤ k ≤ n. The eigenvalue of M_j corresponding to u_j is 1. All other eigenvalues are 0.

The M_j are observables since their eigenvectors form a basis for our quantum state vector space by construction.

The expected value, or expectation, ⟨A⟩ of A given the state...