What are large foundation models and LLMs?
LLMs are deep-learning-based models that use many parameters to learn from vast amounts of unlabeled texts. They can perform various natural language processing tasks such as recognizing, summarizing, translating, predicting, and generating text.
Definition
Deep learning is a branch of machine learning that is characterized by neural networks with multiple layers, hence the term “deep.” These deep neural networks can automatically learn hierarchical data representations, with each layer extracting increasingly abstract features from the input data. The depth of these networks refers to the number of layers they possess, enabling them to effectively model intricate relationships and patterns in complex datasets.
LLMs belong to a wider set of models that feature the AI subfield of generative AI: large foundation models (LFMs). Hence, in the following sections, we will explore the rise and development of LFMs and LLMs, as well as their technical architecture, which is a crucial task to understand their functioning and properly adopt those technologies within your applications.
We will start by understanding why LFMs and LLMs differ from traditional AI models and how they represent a paradigm shift in this field. We will then explore the technical functioning of LLMs, how they work, and the mechanisms behind their outcomes.
AI paradigm shift – an introduction to foundation models
A foundation model refers to a type of pre-trained generative AI model that offers immense versatility by being adaptable for various specific tasks. These models undergo extensive training on vast and diverse datasets, enabling them to grasp general patterns and relationships within the data – not just limited to textual but also covering other data formats such as images, audio, and video. This initial pre-training phase equips the models with a strong foundational understanding across different domains, laying the groundwork for further fine-tuning. This cross-domain capability differentiates generative AI models from standard natural language understanding (NLU) algorithms.
Note
Generative AI and NLU algorithms are both related to natural language processing (NLP), which is a branch of AI that deals with human language. However, they have different goals and applications.
The difference between generative AI and NLU algorithms is that generative AI aims to create new natural language content, while NLU algorithms aim to understand existing natural language content. Generative AI can be used for tasks such as text summarization, text generation, image captioning, or style transfer. NLU algorithms can be used for tasks such as chatbots, question answering, sentiment analysis, or machine translation.
Foundation models are designed with transfer learning in mind, meaning they can effectively apply the knowledge acquired during pre-training to new, related tasks. This transfer of knowledge enhances their adaptability, making them efficient at quickly mastering new tasks with relatively little additional training.
One notable characteristic of foundation models is their large architecture, containing millions or even billions of parameters. This extensive scale enables them to capture complex patterns and relationships within the data, contributing to their impressive performance across various tasks.
Due to their comprehensive pre-training and transfer learning capabilities, foundation models exhibit strong generalization skills. This means they can perform well across a range of tasks and efficiently adapt to new, unseen data, eliminating the need for training separate models for individual tasks.
This paradigm shift in artificial neural network design offers considerable advantages, as foundation models, with their diverse training datasets, can adapt to different tasks based on users’ intent without compromising performance or efficiency. In the past, creating and training distinct neural networks for each task, such as named entity recognition or sentiment analysis, would have been necessary, but now, foundation models provide a unified and powerful solution for multiple applications.
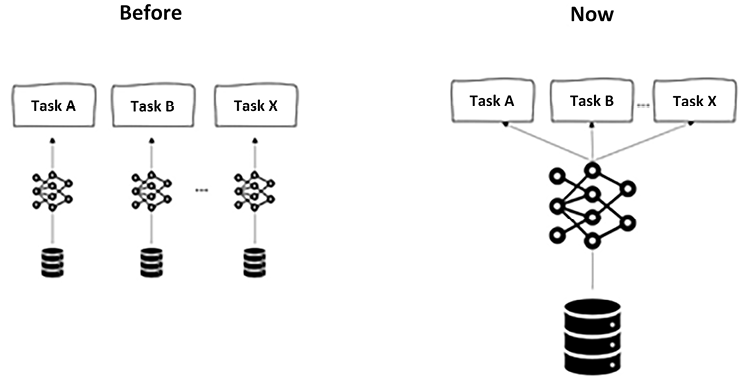
Figure 1.1: From task-specific models to general models
Now, we said that LFMs are trained on a huge amount of heterogeneous data in different formats. Whenever that data is unstructured, natural language data, we refer to the output LFM as an LLM, due to its focus on text understanding and generation.
Figure 1.2: Features of LLMs
We can then say that an LLM is a type of foundation model specifically designed for NLP tasks. These models, such as ChatGPT, BERT, Llama, and many others, are trained on vast amounts of text data and can generate human-like text, answer questions, perform translations, and more.
Nevertheless, LLMs aren’t limited to performing text-related tasks. As we will see throughout the book, those unique models can be seen as reasoning engines, extremely good in common sense reasoning. This means that they can assist us in complex tasks, analytical problem-solving, enhanced connections, and insights among pieces of information.
In fact, as LLMs mimic the way our brains are made (as we will see in the next section), their architectures are featured by connected neurons. Now, human brains have about 100 trillion connections, way more than those within an LLM. Nevertheless, LLMs have proven to be much better at packing a lot of knowledge into those fewer connections than we are.
Under the hood of an LLM
LLMs are a particular type of artificial neural networks (ANNs): computational models inspired by the structure and functioning of the human brain. They have proven to be highly effective in solving complex problems, particularly in areas like pattern recognition, classification, regression, and decision-making tasks.
The basic building block of an ANN is the artificial neuron, also known as a node or unit. These neurons are organized into layers, and the connections between neurons are weighted to represent the strength of the relationship between them. Those weights represent the parameters of the model that will be optimized during the training process.
ANNs are, by definition, mathematical models that work with numerical data. Hence, when it comes to unstructured, textual data as in the context of LLMs, there are two fundamental activities that are required to prepare data as model input:
- Tokenization: This is the process of breaking down a piece of text (a sentence, paragraph, or document) into smaller units called tokens. These tokens can be words, subwords, or even characters, depending on the chosen tokenization scheme or algorithm. The goal of tokenization is to create a structured representation of the text that can be easily processed by machine learning models.

Figure 1.3: Example of tokenization
- Embedding: Once the text has been tokenized, each token is converted into a dense numerical vector called an embedding. Embeddings are a way to represent words, subwords, or characters in a continuous vector space. These embeddings are learned during the training of the language model and capture semantic relationships between tokens. The numerical representation allows the model to perform mathematical operations on the tokens and understand the context in which they appear.
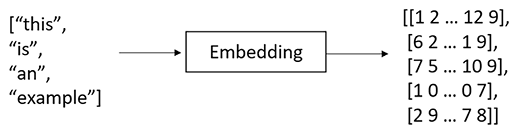
Figure 1.4: Example of embedding
In summary, tokenization breaks down text into smaller units called tokens, and embeddings convert these tokens into dense numerical vectors. This relationship allows LLMs to process and understand textual data in a meaningful and context-aware manner, enabling them to perform a wide range of NLP tasks with impressive accuracy.
For example, let’s consider a two-dimensional embedding space where we want to vectorize the words Man, King, Woman, and Queen. The idea is that the mathematical distance between each pair of those words should be representative of their semantic similarity. This is illustrated by the following graph:
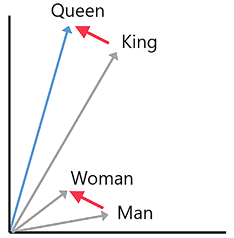
Figure 1.5: Example of words embedding in a 2D space
As a result, if we properly embed the words, the relationship King – Man + Woman ≈ Queen should hold.
Once we have the vectorized input, we can pass it into the multi-layered neural network. There are three main types of layers:
- Input layer: The first layer of the neural network receives the input data. Each neuron in this layer corresponds to a feature or attribute of the input data.
- Hidden layers: Between the input and output layers, there can be one or more hidden layers. These layers process the input data through a series of mathematical transformations and extract relevant patterns and representations from the data.
- Output layer: The final layer of the neural network produces the desired output, which could be predictions, classifications, or other relevant results depending on the task the neural network is designed for.
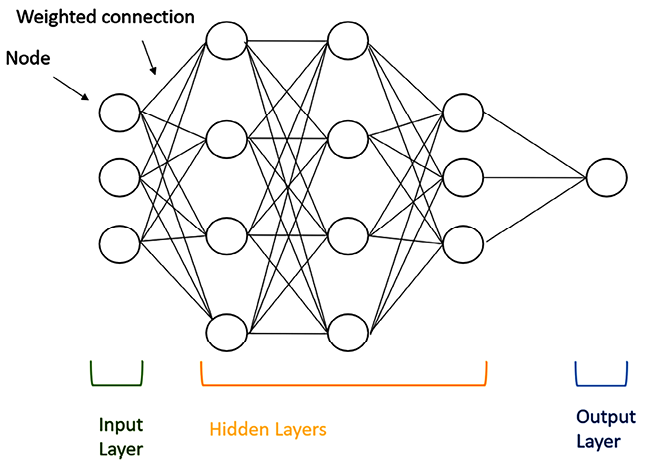
Figure 1.6: High-level architecture of a generic ANN
The process of training an ANN involves the process of backpropagation by iteratively adjusting the weights of the connections between neurons based on the training data and the desired outputs.
Definition
Backpropagation is an algorithm used in deep learning to train neural networks. It involves two phases: the forward pass, where data is passed through the network to compute the output, and the backward pass, where errors are propagated backward to update the network’s parameters and improve its performance. This iterative process helps the network learn from data and make accurate predictions.
During backpropagation, the network learns by comparing its predictions with the ground truth and minimizing the error or loss between them. The objective of training is to find the optimal set of weights that enables the neural network to make accurate predictions on new, unseen data.
ANNs can vary in architecture, including the number of layers, the number of neurons in each layer, and the connections between them.
When it comes to generative AI and LLMs, their remarkable capability of generating text based on our prompts is based on the statistical concept of Bayes’ theorem.
Definition
Bayes’ theorem, named after the Reverend Thomas Bayes, is a fundamental concept in probability theory and statistics. It describes how to update the probability of a hypothesis based on new evidence. Bayes’ theorem is particularly useful when we want to make inferences about unknown parameters or events in the presence of uncertainty. According to Bayes’ theorem, given two events, A and B, we can define the conditional probability of A given B as:
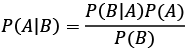
Where:
- P(B|A) = probability of B occurring given A, also known as the likelihood of A given a fixed B.
- P(A|B) = probability of A occurring, given B; also known as the posterior probability of A, given B.
- P(A) and P(B) = probability of observing A or B without any conditions.
Bayes’ theorem relates the conditional probability of an event based on new evidence with the a priori probability of the event. Translated into the context of LLMs, we are saying that such a model functions by predicting the next most likely word, given the previous words prompted by the user.
But how can LLMs know which is the next most likely word? Well, thanks to the enormous amount of data on which LLMs have been trained (we will dive deeper into the process of training an LLM in the next sections). Based on the training text corpus, the model will be able to identify, given a user’s prompt, the next most likely word or, more generally, text completion.
For example, let’s consider the following prompt: “The cat is on the….” and we want our LLM to complete this sentence. However, the LLM may generate multiple candidate words, so we need a method to evaluate which of the candidates is the most likely one. To do so, we can use Bayes’ theorem to select the most likely word given the context. Let’s see the required steps:
- Prior probability P(A): The prior probability represents the probability of each candidate word being the next word in the context, based on the language model’s knowledge learned during training. Let’s assume the LLM has three candidate words: “table,” “chair,” and “roof.”
P(“table”), P(“chain”), and P(“roof”) are the prior probabilities for each candidate word, based on the language model’s knowledge of the frequency of these words in the training data.
- Likelihood (P(B|A)): The likelihood represents how well each candidate word fits the context “The cat is on the....” This is the probability of observing the context given each candidate word. The LLM calculates this based on the training data and how often each word appears in similar contexts.
For example, if the LLM has seen many instances of “The cat is on the table,” it would assign a high likelihood to “table” as the next word in the given context. Similarly, if it has seen many instances of “The cat is on the chair,” it would assign a high likelihood to “chair” as the next word.
P(“The cat is on the table”), P(“The cat is on the chair”), and P(“The cat is on the roof”) are the likelihoods for each candidate word given the context.
- Posterior probability (P(A|B)): Using Bayes’ theorem, we can calculate the posterior probability for each candidate word based on the prior probability and the likelihood:



- Selecting the most likely word. After calculating the posterior probabilities for each candidate word, we choose the word with the highest posterior probability as the most likely next word to complete the sentence.
The LLM uses Bayes’ theorem and the probabilities learned during training to generate text that is contextually relevant and meaningful, capturing patterns and associations from the training data to complete sentences in a coherent manner.
The following figure illustrates how it translates into the architectural framework of a neural network:
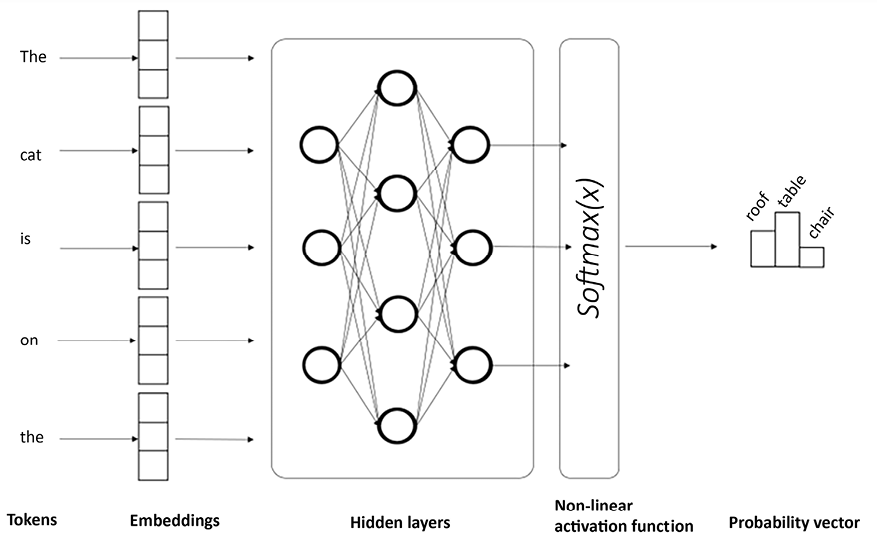
Figure 1.7: Predicting the next most likely word in an LLM
Note
The last layer of the ANN is typically a non-linear activation function. In the above illustration, the function is Softmax, a mathematical function that converts a vector of real numbers into a probability distribution. It is often used in machine learning to normalize the output of a neural network or a classifier. The Softmax function is defined as follows:
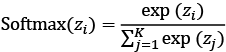
where zi is the i-th element of the input vector, and K is the number of elements in the vector. The Softmax function ensures that each element of the output vector is between 0 and 1 and that the sum of all elements is 1. This makes the output vector suitable for representing probabilities of different classes or outcomes.
Overall, ANNs are the core pillars of the development of generative AI models: thanks to their mechanisms of tokenization, embedding, and multiple hidden layers, they can capture complex patterns even in the most unstructured data, such as natural language.
However, what we are observing today is a set of models that demonstrates incredible capabilities that have never been seen before, and this is due to a particular ANNs’ architectural framework, introduced in recent years and the main protagonist of LLM development. This framework is called the transformer, and we are going to cover it in the following section.






























































