A branch of applied mathematics is mathematical optimization, popularly known as mathematical programming. It finds applications in fields such as manufacturing, inventory control, scheduling, networks, economics, engineering, and financial portfolio allocation. Almost any classification, regression, or clustering problem can be cast as an optimization problem. Some problems are static, while some are dynamic, wherein the values of system variables change over time.
Understanding the problem
Mathematical optimization is basically choosing inputs from a set of allowed options to obtain the optimized or best possible output in a given problem. There are variables, which are essentially the decisions we have to make; constraints, which are the business rules we have to adhere to; and objectives, which are the business goals we are aiming to achieve by representing the real-world business problem as an optimization problem. For example, a hospital’s business problem is equipment and facility capacity planning. Medical equipment including beds and testing kits comprise the decision variables in this case; constraints are conventional and crisis capacity levels and regulations; and finally, the objective is to maximize resource utilization and service performance and minimize operating costs at the same time.
The most basic optimization problem consists of an objective function or cost function, which is the output value we try to optimize, in other words, maximize or minimize. The inputs are variables that can be controlled. Variables can be either discrete or continuous. The scale of a problem is pretty much determined by the dimensionality, that is, the number of scalar variables (also called decision variables) on which the search is performed. Constraints or equations place limits on how big or small some variables can get. Some problems have constraints, which can be equality or inequality constraints, while some problems do not have them at all, which implies the unbounded optimization of the function.
A linear programming problem is an optimization problem wherein the objective function and all constraints are linear, that is, the variables have only first-order terms. It was linear programming that led to the development of optimization in the 1940s. If either the function or one or more constraint(s) is non-linear, then we have a non-linear programming problem. For example, optimizing smooth (well-defined gradient, continuous) functions is easier. Knowing the problem type enables the selection of the right tool to solve it.
Formulation of the problem
The general formulation of a mathematical problem with an objective function f(x) represents questions in terms of variables and constraints. A typical form is as follows:
Minimize f ( such that
such that  where i = 1, 2, ...., m
where i = 1, 2, ...., m
The nature of variables and constraints can be quite diverse. The variables may be discrete, continuous, or sets (groups), and the constraints may be deterministic or stochastic. The objective function may also include dynamic aspects.
Sometimes we are interested in finding the global optimum point without any constraints or restrictions on the region in space. Such problems are unconstrained optimization problems. At other times, we have to solve problems subject to certain constraints, such as restrictions on control variables. For example, in the preceding case, we might have to minimize the function subject to ( . These are constrained optimization problems.
. These are constrained optimization problems.
Example 1:
Let us have multiple (inequalities) constraints with two variables, x and y, as follows:
2x + 3y ≤ 34
3x + 5y ≤ 54
0 ≤ x, y
A graphical optimization would be an overlap (dark region) of the graphs, shown in Figure 1.1. Here the constraints are linear, and therefore, the maximum and minimum must lie on the boundary. And it is most likely that the optimum solution occurs at one of the three specified points. With non-linear constraints, the optimum occurs either at the boundaries or between them. In unconstrained optimization, either the function has no boundaries, or if it has, they are soft.
Figure 1.1: Graphical representation of linear constrained optimization
Typical constraints in business problems involve time, money, and resources while attempting to maximize an objective function. The constraints are more particular to the use case at hand while minimizing an objective function. Suppose in the preceding problem the objective function is linear, such as f(x, y) = 20x + 35y, and the optimum is found out from the slope of the function. If f(x, y) takes a value, the value becomes a boundary, and the constraint plus the boundary make a linear constraint.
With linear constraints, the overlap region is considered to be feasible. Non-linear constraints can be very difficult to visualize as a distorted x-y plane makes it almost impossible to graph the feasible region.
Example 2:
In non-linear constrained optimization, the first step is to start on the boundary of the feasible region. To minimize the objective function, the vector direction should be chosen so that it decreases the function and stays in the feasible region. If the dot product of the gradient (slope) of the objective function with the vector itself is negative at a point on the boundary, then the vector is said to be moving in the descent direction. Also, a vector that does not violate the constraints is said to move in a feasible direction.
Figure 1.2: Feasible direction in non-linear constrained optimization
The constraint equation on the boundary is g(x) =0, shown in Figure 1.2. A feasible vector cannot cause the value of g(x) to increase. It must either remain zero or decrease. If the dot product of the gradient of the constraint with the vector itself is negative or zero at the point, then the vector is said to be moving in a feasible direction. For example, say we have the following objective function:
Minimize 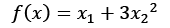
And the initial point (4, 2 on a single constraint:
on a single constraint:
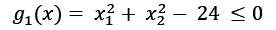
Where  and
and  are the variables, in general, standing for a matrix or array. The vector
are the variables, in general, standing for a matrix or array. The vector <-1, 0> is in both descent and feasible directions. Since the initial point is randomly chosen, there is a good chance that the overlap between the set of all feasible vectors and the set of all descent vectors is large. However, as we approach the minimum, the overlap gets smaller, and at the minimum or optimum point, there is no overlap at all. At the optimum, one cannot minimize the objective function further without violating the constraint. We know we have reached the optimum when the dot product of the two gradients is negative, and the two vectors have a matrix determinant equal to zero.
Another possibility is that the optimum occurs in the interior of the feasible region rather than on the boundary. In such a case, the gradient of the objective function will be zero at that point. The concavity (non-convexity) of the point is determined by the eigenvalues of Hessian (second differential) of the function.
In optimization problems where the objective function is noisy or its gradient is computed numerically as the gradient is not given (complex boundary value problems, for instance), errors are induced. Even if the objective functions themselves are not noisy, gradient-based optimization may turn out to be noisy. There are different optimizers available as library functions with Scientific Python, or scipy for short, to solve such optimization problems, and we will learn about a few of them in the following chapters. Now that we have learned about the concepts of mathematical optimization, we shall explore another concept in mathematical modeling, which is signal processing.
 United States
United States
 Great Britain
Great Britain
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Singapore
Singapore
 Hungary
Hungary
 Ukraine
Ukraine
 Luxembourg
Luxembourg
 Estonia
Estonia
 Lithuania
Lithuania
 South Korea
South Korea
 Turkey
Turkey
 Switzerland
Switzerland
 Colombia
Colombia
 Taiwan
Taiwan
 Chile
Chile
 Norway
Norway
 Ecuador
Ecuador
 Indonesia
Indonesia
 New Zealand
New Zealand
 Cyprus
Cyprus
 Denmark
Denmark
 Finland
Finland
 Poland
Poland
 Malta
Malta
 Czechia
Czechia
 Austria
Austria
 Sweden
Sweden
 Italy
Italy
 Egypt
Egypt
 Belgium
Belgium
 Portugal
Portugal
 Slovenia
Slovenia
 Ireland
Ireland
 Romania
Romania
 Greece
Greece
 Argentina
Argentina
 Netherlands
Netherlands
 Bulgaria
Bulgaria
 Latvia
Latvia
 South Africa
South Africa
 Malaysia
Malaysia
 Japan
Japan
 Slovakia
Slovakia
 Philippines
Philippines
 Mexico
Mexico
 Thailand
Thailand
















