5.3 Linear maps
We’ve looked at linear functions several times to get a concrete idea of how they work. We must generalize this idea to vector spaces.
Let U and V be vector spaces over the same field F. Let u1 and u2 be in U and s1 and s2 be scalars in F.
The function L: U → V is a linear map if

In particular, we have
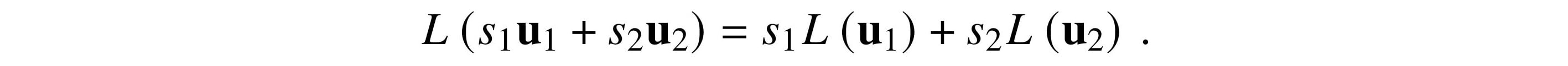
When U = V, we also say L is a linear transformation of U or a linear operator on U. linear$map linear$transformation linear$operator
All linear transformations on R2 look like
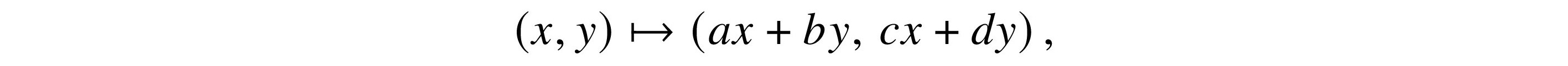
using Cartesian coordinates, and with a, b, c, d, x, and y in R. This is interesting because the linear transformations on R1 all look like the somewhat trivial x ↦ ax.
Exercise 5.2
Show that the function

for a, b, c, d, x, and y in C is a linear transformation of C2.
The linear transformations on R3...























































