5.1 R2 and C1
In section 4.2, we looked at the real plane as a set of standard Cartesian coordinate pairs (x, y) with x and y in R representing points we can plot. We give these pairs an algebraic structure so that if u and v are in R2, then so is u + v. Also, if r is in R, we say that r is a scalar. r u and r v are in R2 as well. We carry out the addition coordinate by coordinate. The multiplication by r, called scalar multiplication, is also done that way. scalar R2 C1
If u = (u1, u2) and v = (v1, v2),
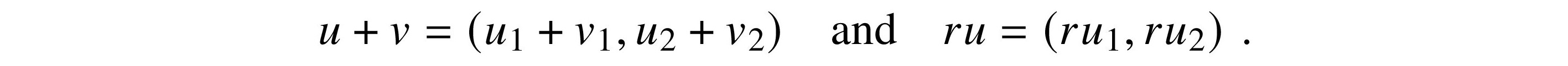
Using the origin O = (0, 0) as the identity element, R2 is a commutative group under addition. With scalar multiplication by elements of the field R, R2 is a two-dimensional vector space over R.
Rather than considering them as pairs or points, we now call u and v vectors. I use bold to indicate a variable or a “point” is a vector. When we plot a vector, we draw it as an arrow from the origin (0, 0) to the point represented...































































