AVL trees
Invented by Georgy Adelson-Velski and Evgenii Landis, and named with their initials, AVL trees were the first self-balance binary search tree created.
AVL tree's special characteristic is if the height of a node subtree is N, the height of the other subtree of the same node must be in the range [N-1, N+1]. This means that heights of both children should differ at most one.
For example, if the height of the right subtree is 3, the height of the left subtree could be 2, 3, or 4. The difference between both heights is called the Balance factor:
Balance factor = Height(RightSubtree) - Height(LeftSubtree)
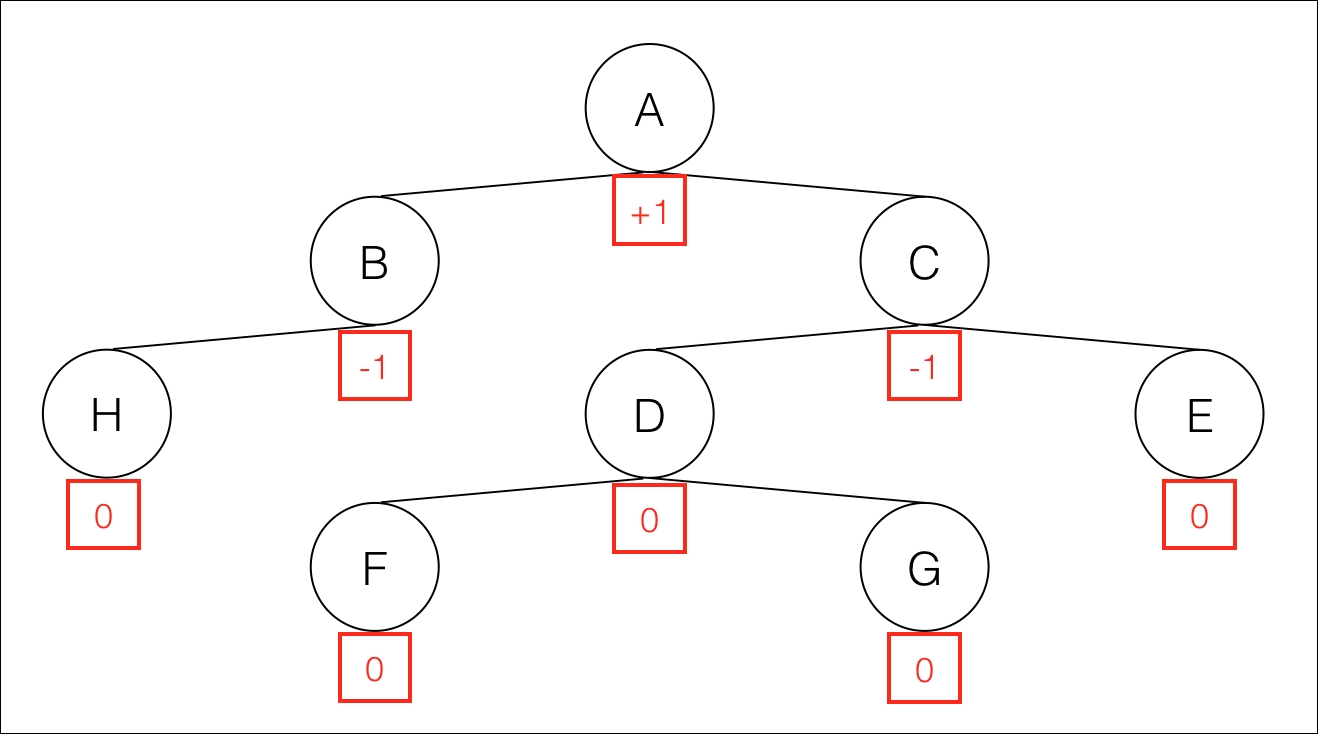
AVL tree example with balance factors of each node
In the preceding figure, the balance factor of a valid AVL tree is in the range [-1, 1] for every node. Leaves have a balance factor of 0.
If Balance factor is < 0, the node is called left heavy
If Balance factor is = 0, the node is called balanced
If Balance factor is > 0, the node is called right heavy
If a child subtree doesn...























































