Probability, odds, and log odds

We are familiar with the basic concept of probability in that the probability of an event occurring can be simply modeled as the number of ways the event can occur divided by all the possible outcomes. For example, if, out of 3,000 people who walked into a store, 1,000 actually bought something, then we could say that the probability of a single person buying an item is as shown:

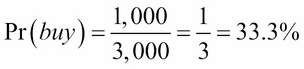
However, we also have a related concept, called odds. The odds of an outcome occurring is the ratio of the number of ways that the outcome occurs divided by every other possible outcome instead of all possible outcomes. In the same example, the odds of a person buying something would be as follows:

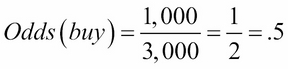
This means that for every customer you convert, you will not convert two customers. These concepts are so related, there is even a formula to get from one to the other. We have that:

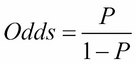
Let's check this with our example, as illustrated:

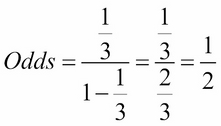
It checks out!

Let's use Python to make a table...