Measuring distances
A metric
on a set S of points is a function  that satisfies these conditions for all x,y,z
∈
S:
that satisfies these conditions for all x,y,z
∈
S:
d(p,q) = 0 ⇔ p=q
d(p,q) = d(p,q)
d(p,q) ≤ d(p,r)+d(r,q)
Normally, we think of the number d(p,q) as the distance between p and q. With that interpretation, the three conditions are obvious: the distance from a point to itself is 0; if the distance between two points is 0, then they must be the same point; the distance from p to q is the same as the distance from q to p; the distance from p to q cannot be greater than the sum of the distances from p to r and from r to q. This last property is called the triangle inequality.
In mathematics, a non-empty set S together with a metric d defined on it is called a metric space. The simplest example is n-dimensional Euclidean space  , where
, where  and d is the Euclidean metric,
and d is the Euclidean metric,
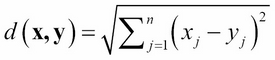
In the case of two dimensions,  , and
, and  . This is just the ordinary distance formula for points in the Cartesian plane, equivalent to the Pythagorean theorem, as Figure...
. This is just the ordinary distance formula for points in the Cartesian plane, equivalent to the Pythagorean theorem, as Figure...



























































