The right model dilemma!
In the previous section, we ran five classification models for the Hypothyroid dataset. Here, the task is to repeat the exercise for four other datasets. It would be a very laborious task to change the code in the appropriate places and repeat the exercise four times over. Thus, to circumvent this problem, we will create a new function referred to as Multiple_Model_Fit. This function will take four arguments: formula, train, testX, and testY. The four arguments have already been set up for each of the five datasets. The function is then set up in a way that generalizes the steps of the previous section for each of the five models.
The function proceeds to create a matrix whose first column consists of the model name, while the second column consists of the accuracy. This matrix is returned as the output of this function:
> Multiple_Model_Fit <- function(formula,train,testX,testY){
+ ntr <- nrow(train) # Training size
+ nte <- nrow(testX) # Test size
+ p <- ncol(testX)
+ testY_numeric <- as.numeric(testY)
+
+ # Neural Network
+ set.seed(12345)
+ NN_fit <- nnet(formula,data = train,size=p,trace=FALSE)
+ NN_Predict <- predict(NN_fit,newdata=testX,type="class")
+ NN_Accuracy <- sum(NN_Predict==testY)/nte
+
+ # Logistic Regressiona
+ LR_fit <- glm(formula,data=train,family = binomial())
+ LR_Predict <- predict(LR_fit,newdata=testX,type="response")
+ LR_Predict_Bin <- ifelse(LR_Predict>0.5,2,1)
+ LR_Accuracy <- sum(LR_Predict_Bin==testY_numeric)/nte
+
+ # Naive Bayes
+ NB_fit <- naiveBayes(formula,data=train)
+ NB_predict <- predict(NB_fit,newdata=testX)
+ NB_Accuracy <- sum(NB_predict==testY)/nte
+
+ # Decision Tree
+ CT_fit <- rpart(formula,data=train)
+ CT_predict <- predict(CT_fit,newdata=testX,type="class")
+ CT_Accuracy <- sum(CT_predict==testY)/nte
+
+ # Support Vector Machine
+ svm_fit <- svm(formula,data=train)
+ svm_predict <- predict(svm_fit,newdata=testX,type="class")
+ svm_Accuracy <- sum(svm_predict==testY)/nte
+
+ Accu_Mat <- matrix(nrow=5,ncol=2)
+ Accu_Mat[,1] <- c("Neural Network","Logistic Regression","Naive Bayes",
+ "Decision Tree","Support Vector Machine")
+ Accu_Mat[,2] <- round(c(NN_Accuracy,LR_Accuracy,NB_Accuracy,
+ CT_Accuracy,svm_Accuracy),4)
+ return(Accu_Mat)
+
+ }
Multiple_Model_Fit is now applied to the Hypothyroid dataset, and the results can be seen to be in agreement with the previous section:
> Multiple_Model_Fit(formula=HT2_Formula,train=HT2_Train,
+ testX=HT2_TestX,
+ testY=HT2_TestY)
[,1] [,2]
[1,] "Neural Network" "0.989"
[2,] "Logistic Regression" "0.9733"
[3,] "Naive Bayes" "0.9733"
[4,] "Decision Tree" "0.9874"
[5,] "Support Vector Machine" "0.9843"The Multiple_Model_Fit function is then applied to the other four classification datasets:
> Multiple_Model_Fit(formula=Waveform_DF_Formula,train=Waveform_DF_Train,
+ testX=Waveform_DF_TestX,
+ testY=Waveform_DF_TestY)
[,1] [,2]
[1,] "Neural Network" "0.884"
[2,] "Logistic Regression" "0.8873"
[3,] "Naive Bayes" "0.8601"
[4,] "Decision Tree" "0.8435"
[5,] "Support Vector Machine" "0.9171"
> Multiple_Model_Fit(formula=GC2_Formula,train=GC2_Train,
+ testX=GC2_TestX,
+ testY =GC2_TestY )
[,1] [,2]
[1,] "Neural Network" "0.7252"
[2,] "Logistic Regression" "0.7572"
[3,] "Naive Bayes" "0.8083"
[4,] "Decision Tree" "0.7061"
[5,] "Support Vector Machine" "0.754"
> Multiple_Model_Fit(formula=ir2_Formula,train=ir2_Train,
+ testX=ir2_TestX,
+ testY=ir2_TestY)
[,1] [,2]
[1,] "Neural Network" "1"
[2,] "Logistic Regression" "1"
[3,] "Naive Bayes" "1"
[4,] "Decision Tree" "1"
[5,] "Support Vector Machine" "1"
> Multiple_Model_Fit(formula=PID_Formula,train=PimaIndiansDiabetes_Train,
+ testX=PimaIndiansDiabetes_TestX,
+ testY=PimaIndiansDiabetes_TestY)
[,1] [,2]
[1,] "Neural Network" "0.6732"
[2,] "Logistic Regression" "0.751"
[3,] "Naive Bayes" "0.7821"
[4,] "Decision Tree" "0.7588"
[5,] "Support Vector Machine" "0.7665"The results for each of the datasets are summarized in the following table:
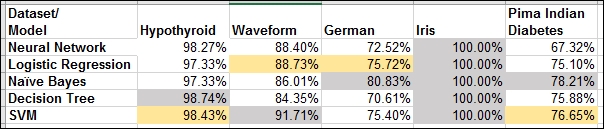
Table 1: Accuracy of five models for five datasets
The iris dataset is a straightforward and simplistic problem, and therefore each of the five models gives us 100% accuracy on the test data. This dataset will not be pursued any further.
For each dataset, we highlight the highest accuracy cell in grey, and highlight the next highest in yellow.
Here is the modeling dilemma. The naïve Bayes method turns out the best for the German and Pima Indian Diabetes datasets. The decision tree gives the highest accuracy for the Hypothyroid dataset, while SVM gives the best results for Waveform. The runner-up place is secured twice by logistic regression and twice by SVM. However, we also know that, depending on the initial seeds and maybe the number of hidden neurons, the neural networks are also expected to perform the best for some datasets. We then also have to consider whether the results will turn out differently for different partitions.
It is in such practical scenarios we would prefer to have a single approach that ensures reasonable properties. With the Hypothyroid dataset, the accuracy for each of the models is 97% or higher, and one might not go wrong with any of the models. However, in the German and Pima Indian Diabetes problems, the maximum accuracy is 80% and 78%, respectively. It would then be better if we can make good use of all the models and build a single unified one with increased accuracy.













































































