A sparse network can be defined as sparse in different aspects of its architecture (Gripon, V., and Berrou, C., 2011). However, the specific type of sparseness we'll look into in this section is the sparseness obtained with respect to the weights of the network, that is, its parameters. We will be looking at each specific parameter to see if it is relatively close to zero (computationally speaking).
Currently, there are three ways of imposing weight sparseness in Keras over Tensorflow, and they are related to the concept of a vector norm. If we look at the Manhattan norm,  , or the Euclidean norm,
, or the Euclidean norm,  , they are defined as follows:
, they are defined as follows:
 ,
,
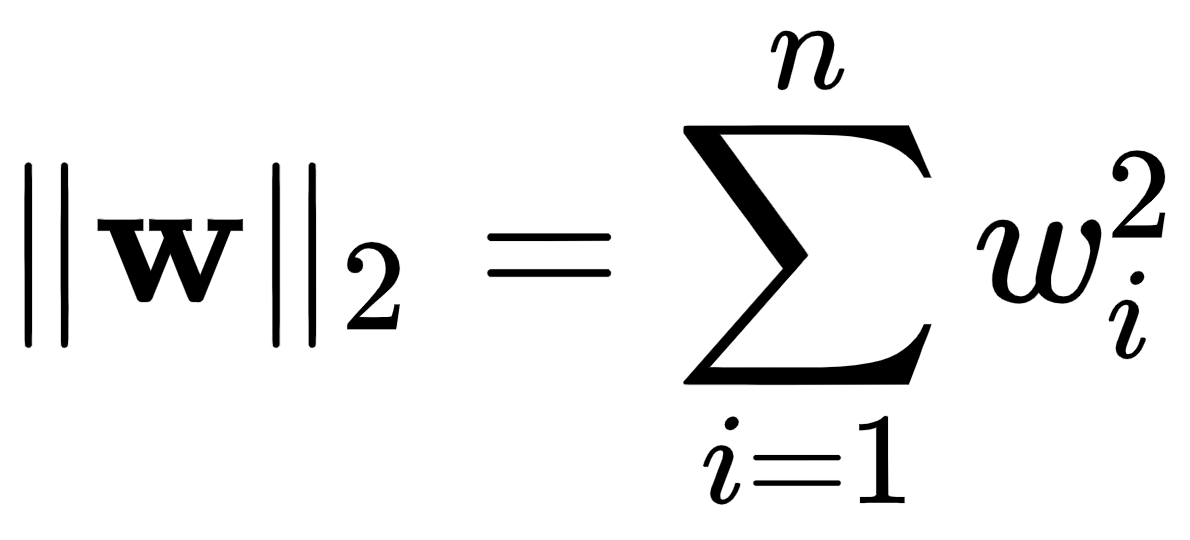
Here, n is the number of elements in the vector  . As you can see, in simple terms, the
. As you can see, in simple terms, the  -norm adds up all elements in terms of their absolute value, while the
-norm adds up all elements in terms of their absolute value, while the  -norm does it in terms of their squared values. It is evident that if both norms are close to zero,
-norm does it in terms of their squared values. It is evident that if both norms are close to zero,  , the chances are that most of its elements are zero or close to zero...
, the chances are that most of its elements are zero or close to zero...












































































