The last method we will implement for our SimpleCNN is the fit method. This function triggers training for our CNN. Our fit method takes four input:
| Argument |
Description |
| X_train |
Training data |
| y_train |
Training labels |
| X_test |
Test data |
| y_test |
Test labels |
The first step of fit is to initialize tf.Graph and tf.Session. Both of these objects are essential to any TensorFlow program. tf.Graph represents the graph in which all the operations for our CNN are defined. You can think of it as a sandbox where we define all the layers and functions. tf.Session is the class that actually executes the operations defined in tf.Graph:
def fit(self, X_train, y_train, X_valid, y_valid):
"""
Trains a CNN on given data
Args:
numpy.ndarrays representing data and labels respectively
"""
graph = tf.Graph()
with graph.as_default():
sess = tf.Session()
We then create datasets using TensorFlow's Dataset API and the _create_tf_dataset method we defined earlier:
train_dataset = self._create_tf_dataset(X_train, y_train)
valid_dataset = self._create_tf_dataset(X_valid, y_valid)
# Creating a generic iterator
iterator = tf.data.Iterator.from_structure(train_dataset.output_types,
train_dataset.output_shapes)
next_tensor_batch = iterator.get_next()
# Separate training and validation set init ops
train_init_ops = iterator.make_initializer(train_dataset)
valid_init_ops = iterator.make_initializer(valid_dataset)
input_tensor, labels = next_tensor_batch
tf.data.Iterator builds an iterator object that outputs a batch of images every time we call iterator.get_next(). We initialize a dataset each for the training and testing data. The result of iterator.get_next() is a tuple of input images and corresponding labels.
The former is input_tensor, which we feed into the build method. The latter is used for calculating the loss function and backpropagation:
num_classes = y_train.shape[1]
# Building the network
logits = self.build(input_tensor=input_tensor, num_classes=num_classes)
logger.info('Built network')
prediction = tf.nn.softmax(logits, name="predictions")
loss_ops = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(
labels=labels, logits=logits), name="loss")
logits (the non-activated outputs of the network) are fed into two other operations: prediction, which is just the softmax over logits to obtain normalized probabilities over the classes, and loss_ops, which calculates the mean categorical cross-entropy between the predictions and the labels.
We then define the backpropagation algorithm used to train the network and the operations used for calculating accuracy:
optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate)
train_ops = optimizer.minimize(loss_ops)
correct = tf.equal(tf.argmax(prediction, 1), tf.argmax(labels, 1), name="correct")
accuracy_ops = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
We are now done building the network along with its optimization algorithms. We use tf.global_variables_initializer() to initialize the weights and operations of our network. We also initialize the tf.train.Saver and tf.summary.FileWriter objects. The tf.train.Saver object saves the weights and architecture of the network, whereas the latter keeps track of various training statistics:
initializer = tf.global_variables_initializer()
logger.info('Initializing all variables')
sess.run(initializer)
logger.info('Initialized all variables')
sess.run(train_init_ops)
logger.info('Initialized dataset iterator')
self.saver = tf.train.Saver()
self.summary_writer = tf.summary.FileWriter(self.logs_path)
Finally, once we have set up everything we need, we can implement the actual training loop. For every epoch, we keep track of the training cross-entropy loss and accuracy of the network. At the end of every epoch, we save the updated weights to disk. We also calculate the validation loss and accuracy every 10 epochs. This is done by calling sess.run(...), where the arguments to this function are the operations that the sess object should execute:
logger.info("Training CNN for {} epochs".format(self.num_epochs))
for epoch_idx in range(1, self.num_epochs+1):
loss, _, accuracy = sess.run([
loss_ops, train_ops, accuracy_ops
])
self._log_loss_and_acc(epoch_idx, loss, accuracy, "train")
if epoch_idx % 10 == 0:
sess.run(valid_init_ops)
valid_loss, valid_accuracy = sess.run([
loss_ops, accuracy_ops
], feed_dict={self.is_training: False})
logger.info("=====================> Epoch {}".format(epoch_idx))
logger.info("\tTraining accuracy: {:.3f}".format(accuracy))
logger.info("\tTraining loss: {:.6f}".format(loss))
logger.info("\tValidation accuracy: {:.3f}".format(valid_accuracy))
logger.info("\tValidation loss: {:.6f}".format(valid_loss))
self._log_loss_and_acc(epoch_idx, valid_loss, valid_accuracy, "valid")
# Creating a checkpoint at every epoch
self.saver.save(sess, self.save_path)
And that completes our fit function. Our final step is to create the script for instantiating the datasets, the neural network, and then running training, which we will write at the bottom of cnn.py.
We will first configure our logger and load the dataset using the Keras fashion_mnist module, which loads the training and testing data:
if __name__ == "__main__":
logging.basicConfig(stream=sys.stdout,
level=logging.DEBUG,
format='%(asctime)s %(name)-12s %(levelname)-8s %(message)s')
logger = logging.getLogger(__name__)
logger.info("Loading Fashion MNIST data")
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
We then apply some simple preprocessing to the data. The Keras API returns numpy arrays of the (Number of images, 28, 28) shape.
However, what we actually want is (Number of images, 28, 28, 1), where the third axis is the channel axis. This is required because our convolutional layers expect input that have three axes. Moreover, the pixel values themselves are in the range of [0, 255]. We will divide them by 255 to get a range of [0, 1]. This is a common technique that helps stabilize training.
Furthermore, we turn the labels, which are simply an array of label indices, into one-hot encodings:
logger.info('Shape of training data:')
logger.info('Train: {}'.format(X_train.shape))
logger.info('Test: {}'.format(X_test.shape))
logger.info('Adding channel axis to the data')
X_train = X_train[:,:,:,np.newaxis]
X_test = X_test[:,:,:,np.newaxis]
logger.info("Simple transformation by dividing pixels by 255")
X_train = X_train / 255.
X_test = X_test / 255.
X_train = X_train.astype(np.float32)
X_test = X_test.astype(np.float32)
y_train = y_train.astype(np.float32)
y_test = y_test.astype(np.float32)
num_classes = len(np.unique(y_train))
logger.info("Turning ys into one-hot encodings")
y_train = np_utils.to_categorical(y_train, num_classes=num_classes)
y_test = np_utils.to_categorical(y_test, num_classes=num_classes)
We then define the input to the constructor of our SimpleCNN. Feel free to tweak the numbers to see how they affect the performance of the model:
cnn_params = {
"learning_rate": 3e-4,
"num_epochs": 100,
"beta": 1e-3,
"batch_size": 32
}
And finally, we instantiate SimpleCNN and call its fit method:
logger.info('Initializing CNN')
simple_cnn = SimpleCNN(**cnn_params)
logger.info('Training CNN')
simple_cnn.fit(X_train=X_train,
X_valid=X_test,
y_train=y_train,
y_valid=y_test)
To run the entire script, all you need to do is run the module:
$ python cnn.py
And that's it! You have successfully implemented a convolutional neural network in TensorFlow to train on the F-MNIST dataset. To track the progress of the training, you can simply look at the output in your terminal/editor. You should see an output that resembles the following:
$ python cnn.py
Using TensorFlow backend.
2018-07-29 21:21:55,423 __main__ INFO Loading Fashion MNIST data
2018-07-29 21:21:55,686 __main__ INFO Shape of training data:
2018-07-29 21:21:55,687 __main__ INFO Train: (60000, 28, 28)
2018-07-29 21:21:55,687 __main__ INFO Test: (10000, 28, 28)
2018-07-29 21:21:55,687 __main__ INFO Adding channel axis to the data
2018-07-29 21:21:55,687 __main__ INFO Simple transformation by dividing pixels by 255
2018-07-29 21:21:55,914 __main__ INFO Turning ys into one-hot encodings
2018-07-29 21:21:55,914 __main__ INFO Initializing CNN
2018-07-29 21:21:55,914 __main__ INFO Training CNN
2018-07-29 21:21:58,365 __main__ INFO Built network
2018-07-29 21:21:58,562 __main__ INFO Initializing all variables
2018-07-29 21:21:59,284 __main__ INFO Initialized all variables
2018-07-29 21:21:59,639 __main__ INFO Initialized dataset iterator
2018-07-29 21:22:00,880 __main__ INFO Training CNN for 100 epochs
2018-07-29 21:24:23,781 __main__ INFO =====================> Epoch 10
2018-07-29 21:24:23,781 __main__ INFO Training accuracy: 0.406
2018-07-29 21:24:23,781 __main__ INFO Training loss: 1.972021
2018-07-29 21:24:23,781 __main__ INFO Validation accuracy: 0.500
2018-07-29 21:24:23,782 __main__ INFO Validation loss: 2.108872
2018-07-29 21:27:09,541 __main__ INFO =====================> Epoch 20
2018-07-29 21:27:09,541 __main__ INFO Training accuracy: 0.469
2018-07-29 21:27:09,541 __main__ INFO Training loss: 1.573592
2018-07-29 21:27:09,542 __main__ INFO Validation accuracy: 0.500
2018-07-29 21:27:09,542 __main__ INFO Validation loss: 1.482948
2018-07-29 21:29:57,750 __main__ INFO =====================> Epoch 30
2018-07-29 21:29:57,750 __main__ INFO Training accuracy: 0.531
2018-07-29 21:29:57,750 __main__ INFO Training loss: 1.119335
2018-07-29 21:29:57,750 __main__ INFO Validation accuracy: 0.625
2018-07-29 21:29:57,750 __main__ INFO Validation loss: 0.905031
2018-07-29 21:32:45,921 __main__ INFO =====================> Epoch 40
2018-07-29 21:32:45,922 __main__ INFO Training accuracy: 0.656
2018-07-29 21:32:45,922 __main__ INFO Training loss: 0.896715
2018-07-29 21:32:45,922 __main__ INFO Validation accuracy: 0.719
2018-07-29 21:32:45,922 __main__ INFO Validation loss: 0.847015
Another thing to check out is TensorBoard, a visualization tool developed by the developers of TensorFlow, to graph the model's accuracy and loss. The tf.summary.FileWriter object we have used serves this purpose. You can run TensorBoard with the following command:
$ tensorboard --logdir=logs/
logs is where our SimpleCNN model writes the statistics to. TensorBoard is a great tool for visualizing the structure of our tf.Graph, as well as seeing how statistics such as accuracy and loss change over time. By default, the TensorBoard logs can be accessed by pointing your browser to localhost:6006:
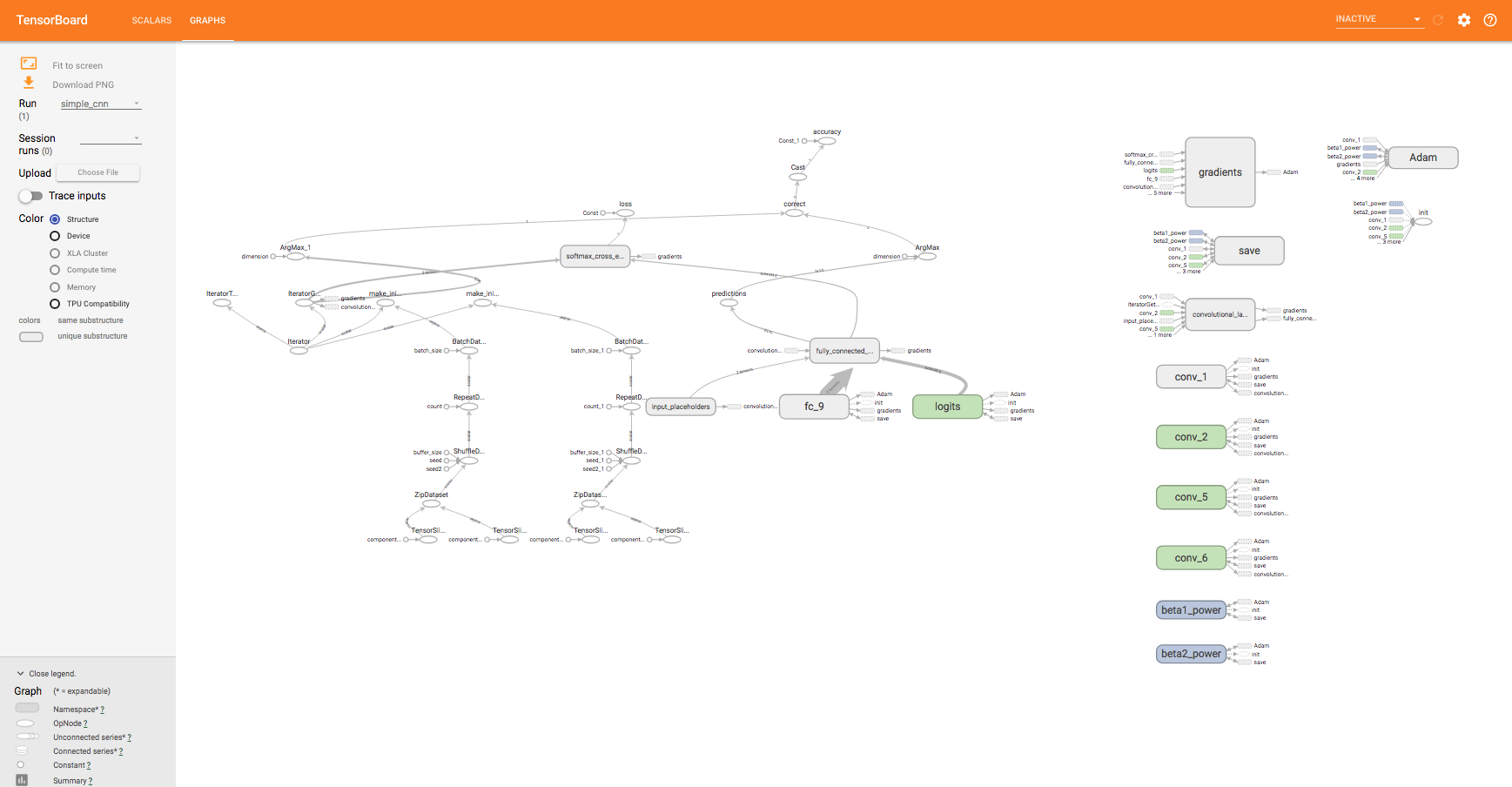
Figure 10: TensorBoard and its visualization of our CNN
Congratulations! We have successfully implemented a convolutional neural network using TensorFlow. However, the CNN we implemented is rather rudimentary, and only achieves mediocre accuracy—the challenge to the reader is to tweak the architecture to improve its performance.






















































 . The output, a, of the perceptron, would be as follows:
. The output, a, of the perceptron, would be as follows:

 are the weights of the perceptron, b is a constant, called the bias, and
are the weights of the perceptron, b is a constant, called the bias, and is the sigmoid activation function that outputs a value between 0 and 1.
is the sigmoid activation function that outputs a value between 0 and 1. would represent a variable, such as the temperature of the current day, humidity, or the weather of the previous day. Then,
would represent a variable, such as the temperature of the current day, humidity, or the weather of the previous day. Then, would compute a value that reflects how likely it is that there will be sunny weather tomorrow. If the model has a good set of values for
would compute a value that reflects how likely it is that there will be sunny weather tomorrow. If the model has a good set of values for  , it is able to make accurate decisions.
, it is able to make accurate decisions.




 , where y is the target function we approximate.
, where y is the target function we approximate.



























