Linear combinations
Once we have established that we can add our vectors and multiply them by scalars, we can start to talk about linear combinations. Linear combinations are just the scaling and addition of vectors to form new vectors. Let's start with our two vectors we have been working with the whole time, |a⟩ and |b⟩. I want to scale my vector |a⟩ by two to get a new vector |c⟩, as shown in the following screenshot:
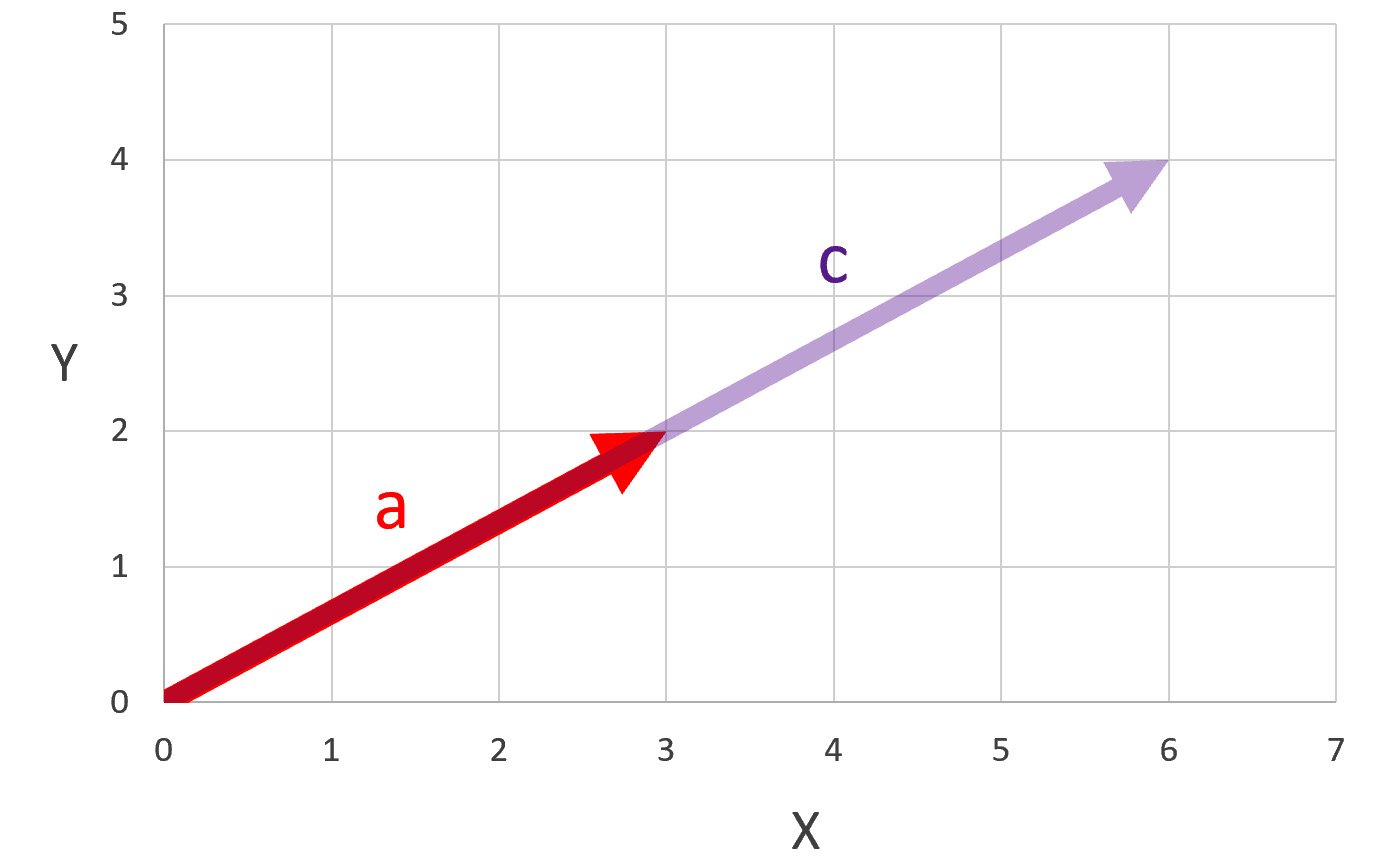
Figure 1.6 – |a⟩ scaled by two to produce |c⟩
As we have said, we can do this algebraically as well, as the following equation shows:

Then, I want to take my vector |b⟩ and scale it by two to get a new vector, |d⟩, as shown in the following screenshot:
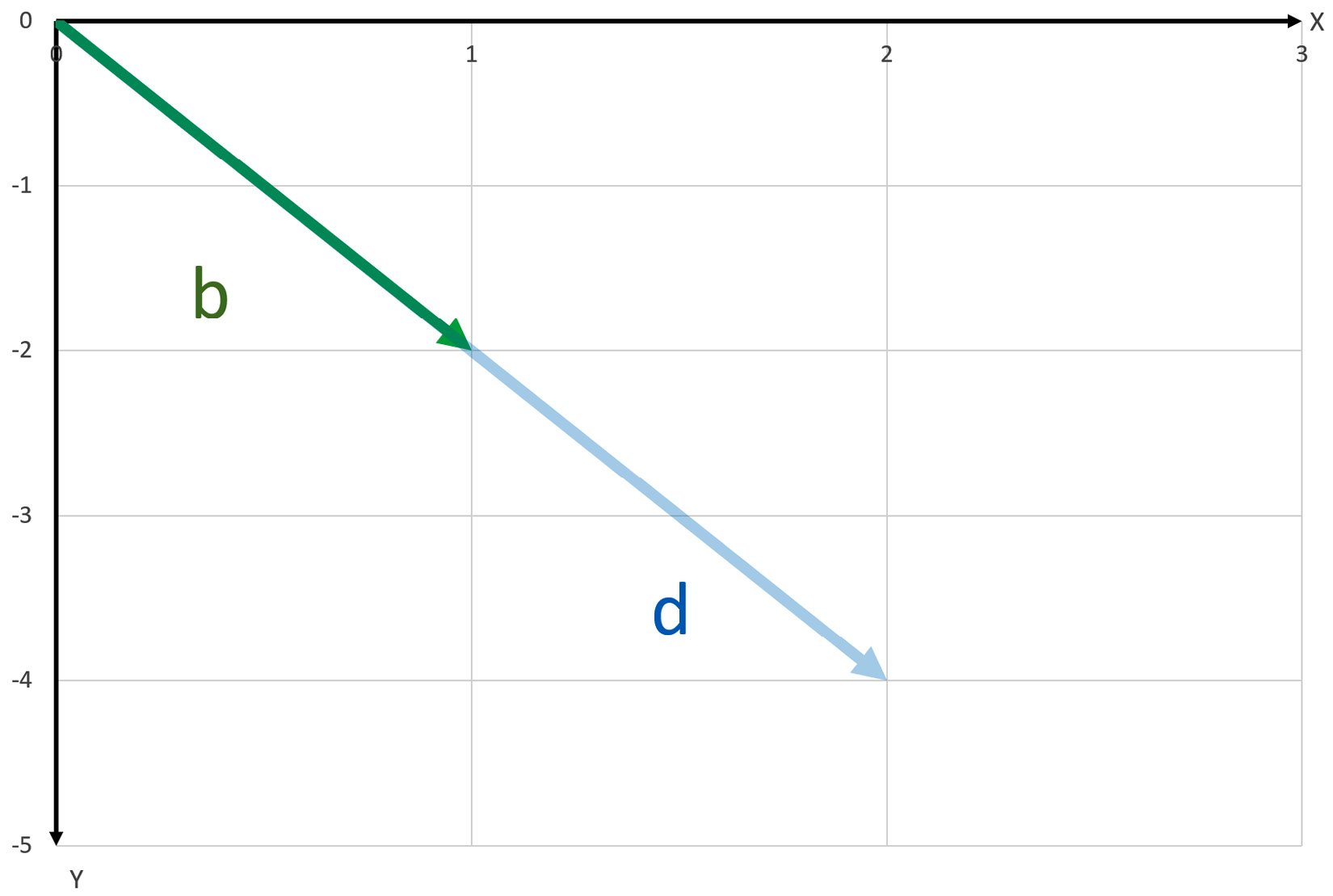
Figure 1.7 – |b⟩ scaled by two to produce |d⟩
So, now, we have a vector |c⟩ that is two times |a⟩, and a vector |d⟩ that is two times |b⟩:

Can I add these two new vectors, |c⟩ and |d⟩? Certainly! I will do that, but I will express |e⟩ as a linear combination of |a⟩ and |b⟩ in the following way:

Vector |e⟩ is a linear combination of vectors |a⟩ and |b⟩! Now, I can show this all geometrically, as follows:
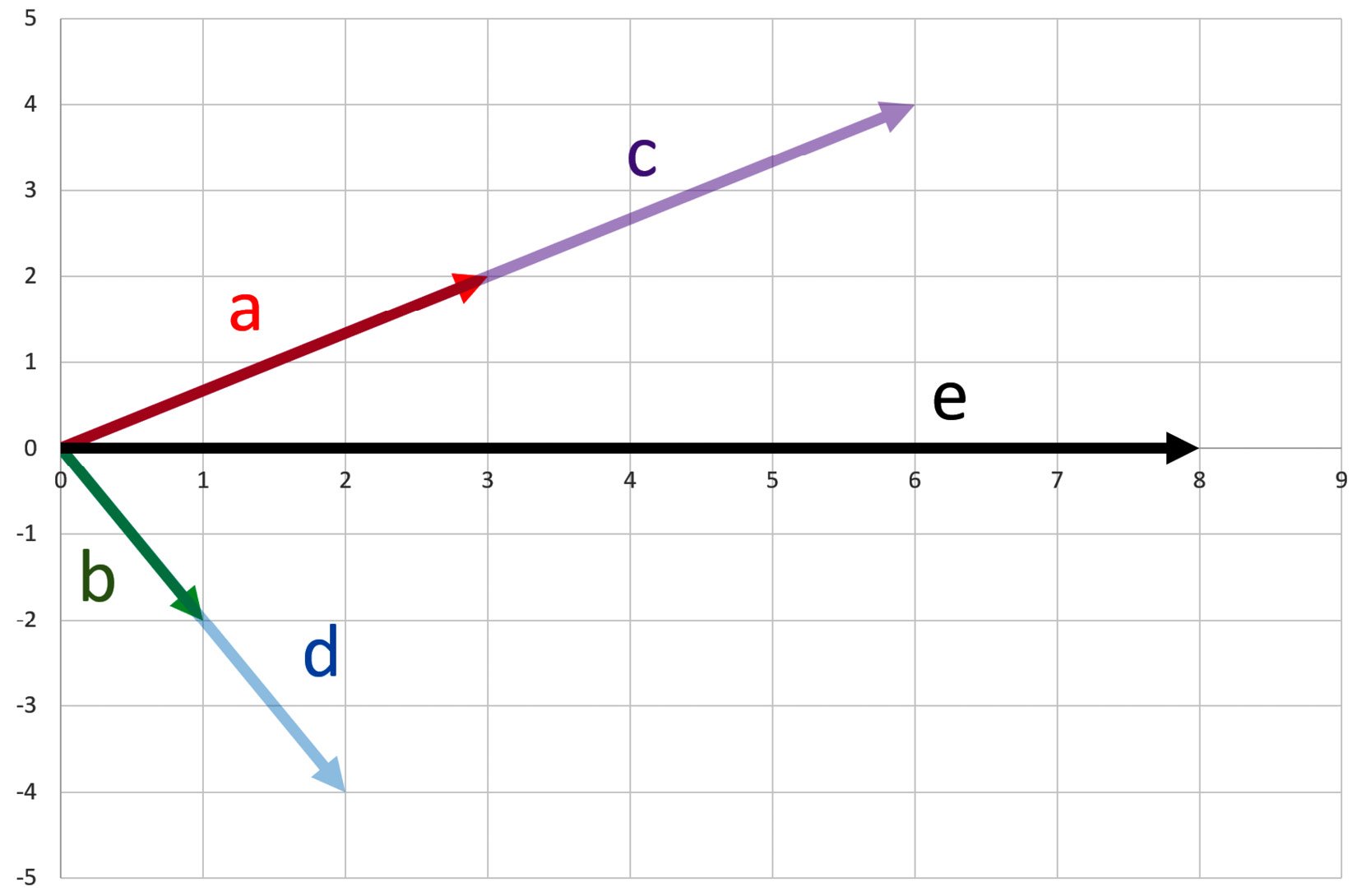
Figure 1.8 – Linear combination
This can also be represented in the following equation:

So, we now have a firm grasp on Euclidean vectors, the algebra you can perform with them, and the concept of a linear combination. We will use that in this next section to describe a quantum phenomenon called superposition.























































