Linear regression is perhaps the most important tool in statistics. It can be used in a wide array of situations and can be easily extended to work in those cases where it can't work in principle. Conceptually, the idea is to model a dependent variable in terms of a set of independent variables and capture coefficients that relate each independent variable to the dependent one. The usual formula here is as follows (assuming that we have one variable and an intercept):
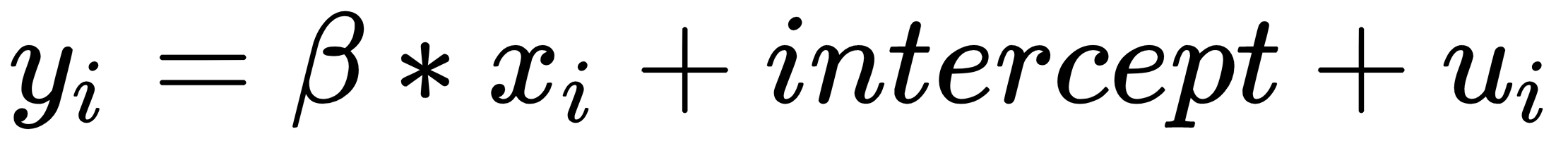
Here, the beta and the intercept are coefficients that we need to find. xi is the independent variable, ui is an unobserved residual, and yi is the target variable. The previous formula can naturally be extended to multiple variables. In that case we would have multiple /beta coefficients.
Maybe the most important aspect of linear regression is that we can do very simple yet powerful interpretations...


























































